Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8 Bài tập - Chủ đề 1 : Định lí Thales

Bài tập 11 trang 69 Tài liệu dạy – học Toán 8 tập 2


Giải bài tập Tam giác ABC có AB = 15, AC = 20, BC = 25. Đường phân giác của góc BAC cắt BC tại D. Qua D vẽ DE // AB (D thuộc AC).

Đề bài

Tam giác ABC có AB = 15, AC = 20, BC = 25. Đường phân giác của góc BAC cắt BC tại D. Qua D vẽ DE // AB (D thuộc AC).

a) Tính độ dài các đoạn thẳng DB, DC và DE.

b) Chứng minh tam giác ABC là tam giác vuông. Tính diện tích tam giác ABC.

c) Tính diện tích các tam giác ADB, ADE và DCE.

Lời giải chi tiết

 

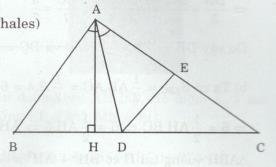
a) ∆ABC có AD là đường phân giác (gt) nên \({{DB} \over {DC}} = {{AB} \over {AC}}\)

\( \Rightarrow {{DB} \over {AB}} = {{DC} \over {AC}} = {{DB + DC} \over {AB + AC}} = {{BC} \over {AB + AC}}\)

Do đó \({{DB} \over {15}} = {{DC} \over {20}} = {{25} \over {15 + 20}} = {5 \over 7}\)

\(\Rightarrow DB = {5 \over 7}.15 = {{75} \over 7},\)

\(DC = {5 \over 7}.20 = {{100} \over 7}\)

∆ABC có DE // AB (gt)

\( \Rightarrow {{DE} \over {AB}} = {{DC} \over {BC}} = {{CE} \over {AC}}\) (hệ quả của định lí Thales)

\( \Rightarrow {{DE} \over {15}} = {{{{100} \over 7}} \over {25}} = {{CE} \over {AC}}\)

\(\Rightarrow {{DE} \over {15}} = {4 \over 7} = {{CE} \over {AC}}.\)

Từ đó ta có: \({{DE} \over {15}} = {4 \over 7}\)

\( \Rightarrow DE = {{15.4} \over 7} = {{60} \over 7}\)

b) Ta có \(B{C^2} = {25^2} = 625\) và \(A{B^2} + A{C^2} = {15^2} + {20^2} = 625\)

Do đó \(B{C^2} = A{B^2} + A{C^2} \Rightarrow \Delta ABC\) vuông tại A (định lí Py-ta-go đảo)

\({S_{ABC}} = {1 \over 2}AB.AC = {1 \over 2}.15.20 = 150(dvdt)\)

c) Kẻ \(AH \bot BC\) tại H

\({S_{ABC}} = {1 \over 2}AH.BC\) và \({S_{ABC}} = 150\)

Suy ra \(150 = {1 \over 2}AH.BC \Rightarrow 150 = {1 \over 2}.AH.25 \)

\(\Rightarrow AH = {{150.2} \over {25}} = 12(cm)\)

\({S_{ADB}} = {1 \over 2}AH.DB = {1 \over 2}.12.{{75} \over 7} = {{450} \over 7}(dvdt)\)

Do đó \({S_{ADC}} = {S_{ABC}} - {S_{ADB}} = 150 - {{450} \over 7} = {{600} \over 7}(dvdt)\)

∆ABC có DE // AB (gt) \( \Rightarrow {{AE} \over {CE}} = {{DB} \over {DC}}\) nên \(\dfrac{{AE}}{{CE}} = \dfrac{{\frac{{75}}{5}}}{{\dfrac{{100}}{7}}} = \dfrac{3}{4}\)

Mà \({{{S_{ADE}}} \over {{S_{DCE}}}} = {{AE} \over {CE}} = {3 \over 4} \Rightarrow {{{S_{ADE}}} \over 3} = {{{S_{DCE}}} \over 4}\)

Do đó \({{{S_{ADE}}} \over 3} = {{{S_{DCE}}} \over 4} = {{{S_{ADE}} + {S_{DCE}}} \over {3 + 4}} = {{{S_{ADC}}} \over 7} = {{600} \over {49}}\)

\( \Rightarrow {S_{ADE}} = {{600} \over {49}}.3 = {{1800} \over {49}}(dvdt)\) và \({S_{DCE}} = {{600} \over {49}}.4 = {{2400} \over {49}}(dvdt)\)

Loigiaihay.com


Bình chọn:
4.1 trên 9 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store