Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9 Bài tập - Chủ đề 6 : Đường kính và dây của đường tròn

Bài 5 trang 128 Tài liệu dạy – học Toán 9 tập 1


Giải bài tập Cho đường tròn (O), bán kính OA = 3 cm.

Đề bài

Cho đường tròn (O), bán kính OA = 3 cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC.

Phương pháp giải - Xem chi tiết

Sử dụng định lí Pytago và quan hệ vuông góc giữa đường kính và dây cung.

Lời giải chi tiết

 

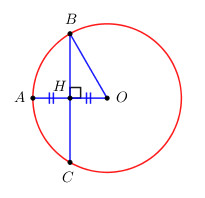
Gọi H là trung điểm của OA. Do H là trung điểm của OA \( \Rightarrow OH = \dfrac{1}{2}OA = \dfrac{3}{2}\,\,\left( {cm} \right)\)

Áp dụng định lí Pytago trong tam giác OBH có:

\(B{H^2} = O{B^2} - O{H^2} \)\(\,= {3^2} - {\left( {\dfrac{3}{2}} \right)^2} = \dfrac{{27}}{4}\)

\(\Leftrightarrow BH = \dfrac{{3\sqrt 3 }}{2}\,\,\left( {cm} \right)\).

Do \(OH \bot BC \Rightarrow H\) là trung điểm của BC (quan hệ vuông góc giữa đường kính và dây cung) \( \Rightarrow BC = 2BH = 3\sqrt 3 \,\,\left( {cm} \right)\).

 Loigiaihay.com


Bình chọn:
4.1 trên 8 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store