Giải SBT đại số, hình học toán lớp 8 tập 1, tập 2

Bài 9. Thể tích của hình chóp đều

Bài 65 trang 151 SBT toán 8 tập 2

Giải bài 65 trang 151 sách bài tập toán 8. 1) Kim tự tháp Kê-ốp (Thế kỉ 25 trước Công nguyên) là một hình chóp tứ giác đều, cạnh đáy bằng 233m, chiều cao hình chóp 146,5m...

Đề bài

1) Kim tự tháp Kê-ốp (Thế kỉ 25 trước Công nguyên) là một hình chóp tứ giác đều, cạnh đáy bằng \(233m\), chiều cao hình chóp \(146,5m.\)

a. Độ dài cạnh bên là bao nhiêu?

b. Tính diện tích xung quanh của hình chóp.

c. Tính thể tích hình chóp.

2) Kim tự tháp Lu-vrơ (Louvre) (Xây dựng vào năm 1988).

Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Lu-vrơ (Pháp). Mô hình có dạng chóp đều chiều cao \(21m,\) độ dài cạnh đáy là \(34m.\)

a. Cạnh bên của hình chóp là bao nhiêu?

b. Tính thể tích hình chóp.

c. Tính tổng diện tích các tấm kính để phủ lên hình chóp này \(({S_{xq}})\).

Phương pháp giải - Xem chi tiết

Sử dụng:

- Thể tích của hình chóp đều bằng một phần ba diện tích mặt đáy nhân với chiều cao.

\(V = \dfrac{1}{3} .S.h\)

Trong đó: \(S\) là diện tích đáy, \(h\) là chiều cao.

- Định lí Pytago trong tam giác vuông: Bình phương của cạnh huyền bằng tổng các bình phương của các cạnh góc vuông.

- Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn.

\({S_{xq}} = pd\)

Trong đó: \(p\) là nửa chu vi đáy, \(d\) là trung đoạn của hình chóp đều.

Lời giải chi tiết

1) Giả sử kim tự tháp Kê-ốp là hình chóp tứ giác đều \(S.ABCD.\)

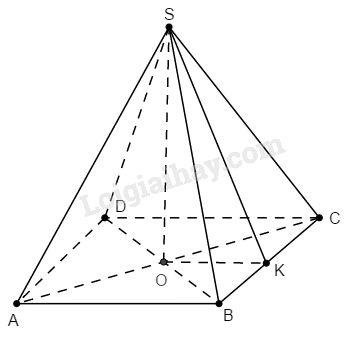
a) Áp dụng định lí Py-ta-go vào tam giác vuông \(AOB\), ta có:

\(O{A^2} + O{B^2} = A{B^2}\)

\( \Rightarrow 2.O{A^2} = A{B^2}\)

\( \displaystyle \Rightarrow O{A^2} = {{A{B^2}} \over 2} =\frac{{{{233}^2}}}{2}= 27144,5\)

Áp dụng định lí Py-ta-go vào tam giác vuông \(SOA\), ta có:

\( S{A^2} = S{O^2} + O{A^2}\)\(\, = 146,{5^2} + 27144,{5} = 48606,75 \)

\( \Rightarrow SA = \sqrt {48606,75} \approx 220,5\;(m). \)

b) Kẻ \(SK ⊥ BC.\)

Vì tam giác \(SBC\) cân tại \(S\) nên \(SK\) vừa là đường cao đồng thời là đường trung tuyến ứng với cạnh đáy \(BC\).

Ta có \(\displaystyle BK = KC = {1 \over 2}BC =\dfrac{{233}}{2}= 116,5\)\(\,(m)\)

Áp dụng định lí Py-ta-go vào tam giác vuông \(SKB\), ta có:

\(S{B^2} = S{K^2} + B{K^2}\)

\( \Rightarrow S{K^2} = S{B^2} - B{K^2} \)\(\, = 48606,75 - 116,5^2 = 35034,5\)

\( \Rightarrow SK = \sqrt {35034,5} \;(m) \)

Diện tích xung quanh của kim tự tháp là:

\(S_{xq} = \left( {233.2} \right).\sqrt {35034,5} \approx 87223,6\)\(\;({m^2})\)

c) Thể tích hình chóp là:

\(V = \displaystyle{1 \over 3}S_{ABCD}.h = \displaystyle{1 \over 3}.233^2.146,5\)\(\, = 2651112,8\;({m^3})\)

2) Giả sử kim tự tháp Lu-vrơ (Louvre) là hình chóp tứ giác đều \(S.ABCD.\)

a) Áp dụng định lí Py-ta-go vào tam giác vuông \(AOB\), ta có:

\(O{A^2} + O{B^2} = A{B^2}\)

\( \Rightarrow 2.O{A^2} = A{B^2}\)

\( \displaystyle \Rightarrow O{A^2} = {{A{B^2}} \over 2} =\frac{{{{34}^2}}}{2}= 578\)

Áp dụng định lí Py-ta-go vào tam giác vuông \(SOA\), ta có:

\( S{A^2} = S{O^2} + O{A^2}\)\(\, = 21{^2} + 578 = 1019 \)

\( \Rightarrow SA = \sqrt {1019} \approx 31,9\;(m). \)

b) Thể tích hình chóp là:

\(V = \displaystyle{1 \over 3}S.h = \displaystyle{1 \over 3}.34^2.21\)\(\, = 8092\;({m^3})\)

c) Kẻ \(SK ⊥ BC.\)

Vì tam giác \(SBC\) cân tại \(S\) nên \(SK\) vừa là đường cao đồng thời là đường trung tuyến ứng với cạnh đáy \(BC\).

Ta có \(\displaystyle BK = KC = {1 \over 2}BC =\dfrac{{34}}{2}= 17\)\(\,(m)\)

Áp dụng định lí Py-ta-go vào tam giác vuông \(SKB\), ta có:

\(S{B^2} = S{K^2} + B{K^2}\)

\( \Rightarrow S{K^2} = S{B^2} - B{K^2} \)\(\, = 1019 - 17^2 = 730\)

\( \Rightarrow SK = \sqrt {730} \;(m) \)

Diện tích xung quanh của kim tự tháp là:

\(S_{xq} = \left( {34.2} \right).\sqrt {730} \approx 1837,3\)\(\;({m^2})\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 66 trang 152 SBT toán 8 tập 2
Giải bài 66 trang 152 sách bài tập toán 8. Thể tích hình chóp đều cho theo các kích thước ở hình 150 là...
Bài 67 trang 152 SBT toán 8 tập 2
Giải bài 67 trang 152 sách bài tập toán 8. Tính thể tích hình chóp tứ giác đều O.ABCD (các kích thước cho trên hình 151)
Bài 68 trang 152 SBT toán 8 tập 2
Giải bài 68 trang 152 sách bài tập toán 8. Hình chóp tứ giác đều có độ dài cạnh bên là 5cm, chiều cao hình chóp là 4cm. Thể tích của hình chóp là ...
Bài 69 trang 152 SBT toán 8 tập 2
Giải bài 69 trang 152 sách bài tập toán 8. Tính diện tích toàn phần của hình chóp đều sau đây ...
Bài 70 trang 153 SBT toán 8 tập 2
Giải bài trang sách bài tập toán 8. Tính thể tích và diện tích toàn phần các hình chóp đều dưới đây (theo các kích thước cho trên hình vẽ 153).
Bài 71 trang 153 SBT toán 8 tập 2
Giải bài 71 trang 153 sách bài tập toán 8. Tính diện tích toàn phần của hình chóp cụt đều cho theo các kích thước trên hình 154.
Bài 72 trang 153 SBT toán 8 tập 2
Giải bài 72 trang 153 sách bài tập toán 8. Cho hình chóp cụt tứ giác đều ABCD.A1B1C1D1 có các cạnh đáy 5cm và 10cm, đường cao của mặt bên bằng 5cm...
Bài 64 trang 151 SBT toán 8 tập 2
Giải bài 64 trang 151 sách bài tập toán 8. Hình 149 là chiếc lều ở một trại hè với các kích thước cho trên hình.
Bài 63 trang 151 SBT toán 8 tập 2
Giải bài 63 trang 151 sách bài tập toán 8. Một cái nhà kính trồng cây thí nghiệm có dạng một lăng trụ đứng có các kích thước như ở hình 148. EDC là một tam giác cân ...
Bài 62 trang 150 SBT toán 8 tập 2
Giải bài 62 trang 150 sách bài tập toán 8. Một hình chóp tứ giác đều và một lăng trụ đứng tứ giác đều như hình 147 dưới đây (cạnh đáy và chiều cao bằng nhau)