Bài 6. Tính chất ba đường phân giác của tam giác

Bài 45 trang 46 SBT toán 7 tập 2

Giải bài 45 trang 46 sách bài tập toán 7. Cho tam giác ABC cân tại A. Gọi G là trọng tâm của tam giác, gọi I là giao điểm các đường phân giác của tam giác. Chứng minh rằng ba điểm A, G, I thẳng hàng.

Đề bài

Cho tam giác \(ABC\) cân tại \(A.\) Gọi \(G\) là trọng tâm của tam giác, gọi \(I\) là giao điểm các đường phân giác của tam giác. Chứng minh rằng ba điểm \(A, G, I\) thẳng hàng.

Phương pháp giải - Xem chi tiết

Sử dụng: Trong một tam giác cân, đường phân giác xuất phát từ đỉnh đồng thời là đường trung tuyến ứng với cạnh đáy

Lời giải chi tiết

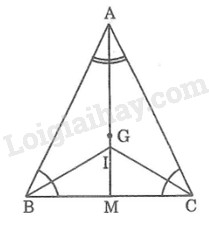
Kẻ đường phân giác của \(\widehat A\) và \(\widehat C\) cắt nhau tại \(I, AI\) cắt \(BC\) tại \(M.\)

Vì \(∆ABC\) cân tại \(A\) nên đường phân giác \(AI\) cũng là đường trung tuyến (tính chất tam giác cân)

Vì \(G\) là trọng tâm của \(∆ABC \)

\(\Rightarrow G ∈\) đường trung tuyến \(AI\)

Vậy \(A, I, G\) thẳng hàng.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.5 trên 21 phiếu

Bài tiếp theo

Bài 46 trang 46 SBT toán 7 tập 2
Giải bài 46 trang 46 sách bài tập toán 7. Cho tam giác ABC. Hãy tìm một điểm sao cho khoảng cách từ điểm đó đến mỗi đoạn thẳng AB, BC, CA là bằng nhau, đồng thời khoảng cách này là ngắn nhất.
Bài 47 trang 46 SBT toán 7 tập 2
Giải bài 47 trang 46 sách bài tập toán 7. Tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác. Chứng minh rằng tam giác đó là tam giác cân.
Bài 48 trang 46 SBT toán 7 tập 2
Giải bài 48 trang 46 SBT toán 7. Cho tam giác ABC cân tại A. Các đường phân giác BD, CE cắt nhau ở K. Chứng minh rằng AK đi qua trung điểm của BC.
Bài 49 trang 46 SBT toán 7 tập 2
Bài 49 trang 46 sách bài tập toán 7. Cho tam giác ABC cân tại A, D là trung điểm của BC. Gọi E và F là chân các đường vuông góc kẻ từ D đến AB và AC. Chứng minh rằng DE = DF.
Bài 50 trang 46 SBT toán 7 tập 2
Giải bài 50 trang 46 sách bài tập toán 7. Cho tam giác ABC có góc A = 70°, các đường phân giác BD, CE cắt nhau ở I. Tính góc BIC.
Bài 51 trang 46 SBT toán 7 tập 2
Giải bài 51 trang 46 sách bài tập toán 7. Tính góc A của tam giác ABC biết rằng các đường phân giác BD, CE cắt nhau tại I trong đó góc BIC bằng: a) 120° b) ∝(∝ > 90°)
Bài 52 trang 46 SBT toán 7 tập 2
Giải bài 52 trang 46 sách bài tập toán 7. Cho tam giác ABC. Các tia phân giác các góc A và C cắt nhau ở I. Các đường phân giác các góc ngoài tại đỉnh A và C cắt nhau ở K. Chứng minh rằng ba điểm B, I, K thẳng hàng.
Bài 53* trang 46 SBT toán 7 tập 2
Giải bài 53* trang 46 sách bài tập toán 7. Cho tam giác ABC vuông tại A. Các tia phân giác của các góc B và C cắt nhau tại I. Gọi D và E là chân các đường vuông góc kẻ từ I đến AB và AC. a) Chứng minh rằng AD = AE.
Bài 6.1, 6.2, 6.3, 6.4 phần bài tập bổ sung trang 47 SBT toán 7 tập 2
Giải bài 6.1, 6.2, 6.3, 6.4 phần bài tập bổ sung trang 47 sách bài tập toán 7. Cho tam giác ABC. Trên tia phân giác của góc B, lấy điểm O nằm trong tam giác ABC sao cho O cách đều hai cạnh AB, AC. Khẳng định nào sau đây sai?...