Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2 Bài 2. Hình nón. Hình nón cụt. Diện tích xung quanh và..

Bài 20 trang 168 SBT toán 9 tập 2


Giải bài 20 trang 168 sách bài tập toán 9. Hình 98 có một hình nón, bán kính đường tròn đáy là m/2 (cm), chiều cao là 2l (cm) và một hình trụ, bán kính đường tròn đáy m (cm), chiều cao 2l (cm).

Đề bài

Hình 98 có một hình nón, bán kính đường tròn đáy là \(\displaystyle {m \over 2}(cm)\), chiều cao là \(2l \;(cm)\) và một hình trụ, bán kính đường tròn đáy \(m \;(cm)\), chiều cao \(2l\; (cm)\).

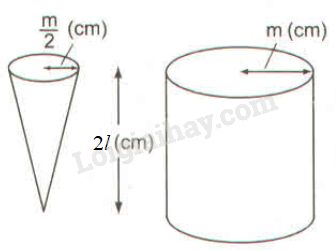
Người ta múc đầy nước vào hình nón và đổ vào hình trụ (không chứa gì cả) thì độ cao của nước trong hình trụ là:

(A) \(\displaystyle {l \over 6}\)(cm);                           (B) \(l\; (cm)\);

(C) \(\displaystyle {5 \over 6}\) (cm);                          (D) \(\displaystyle {{11} \over 6}l\) (cm).

Hãy chọn kết quả đúng.

Phương pháp giải - Xem chi tiết

Sử dụng:

- Thể tích hình nón: \(\displaystyle V = {1 \over 3}\pi {r^2}h\).

(\(r\) là bán kính đường tròn đáy, \(h\) là chiều cao).

- Thể tích hình trụ: \(V= Sh = πr^2h\).

(\(r\) là bán kính đường tròn đáy, \(h\) là chiều cao, \(S\) là diện tích đáy).

Lời giải chi tiết

Thể tích hình nón là: \(\displaystyle V_1={1 \over 3}\pi {r^2}.h\)

\(\displaystyle V_1={1 \over 3}\pi {\left( {{m \over 2}} \right)^2}.2l = {1 \over 3}\pi {{{m^2}} \over 4}.2l \)\(\,\displaystyle = {{\pi {m^2}l} \over 6}\) \((cm^3)\)

Thể tích hình trụ là: \({V_2} = \pi {r^2}.h\)

\({V_2} = \pi {m^2}.2l = 2\pi {m^2}l\) \((cm^3)\)

\(\displaystyle {{{V_1}} \over {{V_2}}} = {{\pi {m^2}l} \over 6}:2\pi {m^2}l\)\(\,\displaystyle  = {{\pi {m^2}l} \over 6}.{1 \over {2\pi {m^2}l}} \)\(\,\displaystyle = {1 \over {12}}\)

Vậy khi đổ đầy nước vào hình nón rồi đổ vào hình trụ thì độ cao của nước trong hình trụ là \(\displaystyle {1 \over {12}}.2l = {1 \over 6}l\) (\(cm\)).

Chọn (A).

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Bài 21 trang 168 SBT toán 9 tập 2

    Giải bài 21 trang 168 sách bài tập toán 9. Nếu chiều cao và bán kính đáy của một hình nón đều tăng lên và bằng 5/4 so với các kích thước tương ứng ban đầu thì trong các tỉ số sau đây ...

  • Bài 22 trang 168 SBT toán 9 tập 2

    Giải bài 22 trang 168 sách bài tập toán 9. Từ một hình nón, người thợ tiện có thể tiện ra một hình trụ cao nhưng “ hẹp” hoặc một hình trụ rộng nhưng “ thấp”. Trong trường hợp nào thì người thợ tiện loại bỏ ít vật liệu hơn?

  • Bài 23 trang 168 SBT toán 9 tập 2

    Giải bài 23 trang 168 sách bài tập toán 9. Hình 99 là một hình nón. Chiều cao là h (cm), bán kính đường tròn đáy là r (cm) và độ dài đường sinh m (cm) thì thể tích hình nón này là ...

  • Bài 24 trang 169 SBT toán 9 tập 2

    Giải bài 24 trang 169 sách bài tập toán 9. Một hình trụ có bán kính đáy 1cm và chiều cao 2cm, người ta khoan đi một phần có dạng hình nón như hình vẽ (h.100) thì phần thể tích còn lại của nó sẽ là ...

  • Bài 25 trang 169 SBT toán 9 tập 2

    Giải bài 25 trang 169 sách bài tập toán 9. Cho tam giác ABC vuông tại A. Gọi V1, V2, V3 theo thứ tự là thể tích của những hình sinh ra khi quay tam giác ABC một vòng xung quanh các cạnh BC, AB và AC...

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store