-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11
-
HÌNH HỌC - TOÁN 11
-
CHƯƠNG I. PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG TRONG MẶT PHẲNG
-
CHƯƠNG II. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
- Bài 1. Đại cương về đường thẳng và mặt phẳng
- Bài 2. Hai đường thẳng chéo nhau và hai đường thẳng song song
- Bài 3. Đường thẳng và mặt phẳng song song
- Bài 4. Hai mặt phẳng song song
- Bài 5. Phép chiếu song song. Hình biểu diễn của một hình không gian
- Ôn tập chương II - Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
-
CHƯƠNG III. VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
-
ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 11
-
-
Câu hỏi tự luyện Toán 11
-
TẢI 50 ĐỀ KIỂM TRA 15 PHÚT TOÁN 11
-
TẢI 30 ĐỀ KIỂM TRA 1 TIẾT TOÁN 11
-
TẢI 5 ĐỀ THI GIỮA KÌ 1 TOÁN 11
-
TẢI 25 ĐỀ THI HỌC KÌ 1 TOÁN 11
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 11
-
TẢI 20 ĐỀ THI HỌC KÌ 2 TOÁN 11
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Bài 1. Vectơ trong không gian
Bài 9 trang 92 SGK Hình học 11
Cho tam giác ABC. Lấy điểm S nằm ngoài mặt phẳng (ABC)...
Đề bài
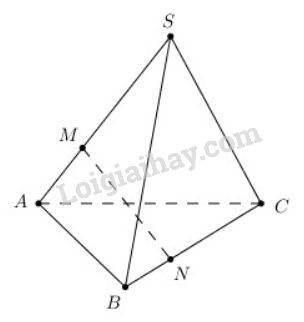
Cho tam giác \(ABC\). Lấy điểm \(S\) nằm ngoài mặt phẳng \((ABC)\). Trên đoạn \(SA\) lấy điểm \(M\) sao cho \(\overrightarrow{MS}\) = \(-2\overrightarrow{MA}\) và trên đoạn \(BC\) lấy điểm \(N\) sao cho \(\overrightarrow{NB}=-\dfrac{1}{2}\overrightarrow{NC}.\) Chứng minh rằng ba véctơ \(\overrightarrow{AB}\), \(\overrightarrow{MN}\), \(\overrightarrow{SC}\) đồng phẳng.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng kết quả của định lí 1 về điều kiện để ba vector đồng phẳng.
Trong không gian cho hai vector \(\overrightarrow a ;\,\,\overrightarrow b \) không cùng phương và vector \(\overrightarrow c \). Khi đó ba vector \(\overrightarrow a ;\,\,\overrightarrow b ;\,\,\overrightarrow c \) đồng phẳng khi và chỉ khi tồn tại cặp số \(m;n\) sao cho \(\overrightarrow c = m\overrightarrow a + n\overrightarrow b \). Ngoài ra cặp số \(m;n\) là duy nhất.
Lời giải chi tiết
Biểu diễn \(\overrightarrow {MN} \) qua hai véc tơ \(\overrightarrow {AB} ,\overrightarrow {SC} \):
Ta có:
\( \overrightarrow {MN} = \overrightarrow {MS} + \overrightarrow {SC} + \overrightarrow {CN} \)\(= {2 \over 3}\overrightarrow {AS} + \overrightarrow {SC} + {2 \over 3}\overrightarrow {CB} \,\,\,\,\,\,\,\,\,\left( 1 \right) \)
\(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN}\)\( = - {1 \over 3}\overrightarrow {AS} + \overrightarrow {AB} - {1 \over 3}\overrightarrow {CB} \,\,\,\left( 2 \right) \)
Nhân (2) với \(2\) rồi cộng với (1) ta được:
\(3\overrightarrow{MN}\) = \(\overrightarrow{SC}\) + \(2\overrightarrow{AB}\) \(\Leftrightarrow\overrightarrow{MN}= \frac{1}{3}\overrightarrow{SC}+\frac{2}{3}\overrightarrow{AB}.\)
Vậy \(\overrightarrow{AB}\), \(\overrightarrow{MN}\), \(\overrightarrow{SC}\) đồng phẳng.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 10 trang 92 SGK Hình học 11
- Bài 8 trang 92 SGK Hình học 11
- Bài 7 trang 92 SGK Hình học 11
- Bài 6 trang 92 SGK Hình học 11
- Bài 5 trang 92 SGK Hình học 11
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
