-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11
-
HÌNH HỌC - TOÁN 11
-
CHƯƠNG I. PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG TRONG MẶT PHẲNG
-
CHƯƠNG II. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
- Bài 1. Đại cương về đường thẳng và mặt phẳng
- Bài 2. Hai đường thẳng chéo nhau và hai đường thẳng song song
- Bài 3. Đường thẳng và mặt phẳng song song
- Bài 4. Hai mặt phẳng song song
- Bài 5. Phép chiếu song song. Hình biểu diễn của một hình không gian
- Ôn tập chương II - Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
-
CHƯƠNG III. VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
-
ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 11
-
-
Câu hỏi tự luyện Toán 11
-
TẢI 50 ĐỀ KIỂM TRA 15 PHÚT TOÁN 11
-
TẢI 30 ĐỀ KIỂM TRA 1 TIẾT TOÁN 11
-
TẢI 5 ĐỀ THI GIỮA KÌ 1 TOÁN 11
-
TẢI 25 ĐỀ THI HỌC KÌ 1 TOÁN 11
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 11
-
TẢI 20 ĐỀ THI HỌC KÌ 2 TOÁN 11
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Ôn tập chương II - Đường thẳng và mặt phẳng trong không..
Bài 8 trang 80 SGK Hình học 11
Với giả thiết của bài tập 7, chu vi của thiết diện tính theo AM = x là:
Đề bài
Với giả thiết của bài tập 7, chu vi của thiết diện tính theo \(AM = x\) là:
(A) \(x( 1 + \sqrt3)\); (B) \(2x ( 1 + \sqrt3)\);
(C) \(3x ( 1 + \sqrt 3)\); (D) Không tính được.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng định lí Ta-let tính các cạnh của tam giác \(MNP\).
Quảng cáo
Lời giải chi tiết
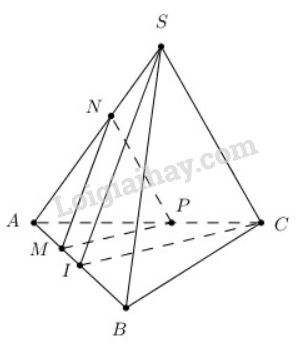
Tam giác \(ABC\) đều có \(I\) là trung điểm \(AB\) nên \(CI\bot AB\).
Tam giác \(AIC\) vuông tại \(I\) nên \( \Rightarrow IC =AC\sin 60^0= {{a\sqrt 3 } \over 2}\)
Ta có: \(MP//IC \Rightarrow \dfrac{{AM}}{{AI}} = \dfrac{{MP}}{{IC}} \) \(\Rightarrow MP = \dfrac{{AM.IC}}{{AI}} = \dfrac{{x.\frac{{a\sqrt 3 }}{2}}}{{\frac{a}{2}}} = x\sqrt 3 \)
\( \Rightarrow MP = MN = x\sqrt 3 \)
Áp dụng định lí Ta-let trong tam giác SAC có \(\displaystyle {{NP} \over {SC}} = {{AP} \over {AC}} = {{AM} \over {AI}}\) \( \displaystyle \Rightarrow NP = SC.{{AM} \over {AI}} = a.{x \over {{a \over 2}}} = 2x\)
Vậy chu vi tam giác \(MNP\) là:
\(MN + MP + NP \) \(= x\sqrt 3 + x\sqrt 3 + 2x \) \(= 2x\left( {1 + \sqrt 3 } \right)\)
Chọn đáp án B.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 9 trang 80 SGK Hình học 11
- Bài 10 trang 80 SGK Hình học 11
- Bài 11 trang 80 SGK Hình học 11
- Bài 12 trang 80 SGK Hình học 11
- Phương pháp xác định thiết diện của hình chóp
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
