Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học Ôn tập chương II - Đường thẳng và mặt phẳng trong không..

Bài 5 trang 79 SGK Hình học 11


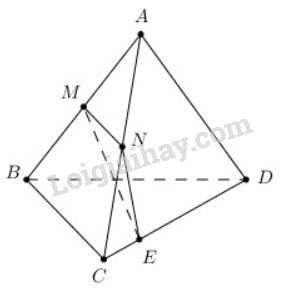
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và AC (h.2.76), E là điểm trên cạnh CD với ED = 3EC.

Đề bài

Cho tứ diện \(ABCD\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(AC\) (h.2.76), \(E\) là điểm trên cạnh \(CD\) với \(ED = 3EC\). Thiết diện tạo bởi mặt phẳng \((MNE)\) và tứ diện \(ABCD\) là:

(A) Tam giác \(MNE\);

(B) Tứ giác \(MNEF\) với \(F\) là điểm bất kì trên cạnh \(BD\);

(C) Hình bình hành \(MNEF\) với \(F\) là điểm trên cạnh \(BD\) mà \(EF // BC\);

(D) Hình thang \(MNEF\) với \(F\) là điểm trên cạnh \(BD\) mà \(EF // BC\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Sử dụng tính chất: Nếu hai mặt phẳng chứa hai đường thẳng song song thì cắt nhau theo giao tuyến song song với hai đường thẳng đó.

Lời giải chi tiết

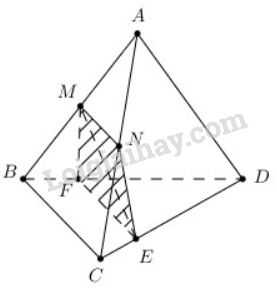
Ta có: \(MN\) là đường trung bình của tam giác \(ABC \Rightarrow MN // BC\).

\(\left\{ \begin{array}{l}\left( {BCD} \right) \supset BC\\\left( {MNE} \right) \supset MN\\MN//BC\\E \in \left( {MNE} \right) \cap \left( {BCD} \right)\end{array} \right. \)

\(\Rightarrow \) giao tuyến của hai mặt phẳng \((MNE)\) và \((BCD)\) là đường thẳng qua \(E\) và song song với \(BC\).

Đường thẳng này cắt \(BD\) tại \(F\). Do đó \(MN//EF//BC\).

Ta có \(MN = \frac{1}{2}BC\).

Áp dụng định lí Ta-let trong tam giác \(BCD\) ta có: \(\frac{{EF}}{{BC}} = \frac{{DE}}{{DC}} = \frac{3}{4} \) \(\Rightarrow EF = \frac{3}{4}BC \Rightarrow MN \ne EF\).

Vậy \(MNEF\) là hình thang.

Chọn đáp án D.

 Loigiaihay.com


Bình chọn:
4.3 trên 6 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store