Bài 7 trang 120 SGK Hình học 11

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a...

Đề bài

Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $3a$ , cạnh bên bằng $2a$ . Tính khoảng cách từ $S$ tới mặt đáy $(ABC)$ .

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Gọi H là tâm tam giác đều ABC $\Rightarrow SH \, \bot \, \left( {ABC} \right) \Rightarrow d\left( {S;\left( {ABC} \right)} \right) = SH$

Áp dụng định lí Pytago trong tam giác vuông để tính $SH$ .

Quảng cáo

Lời giải chi tiết

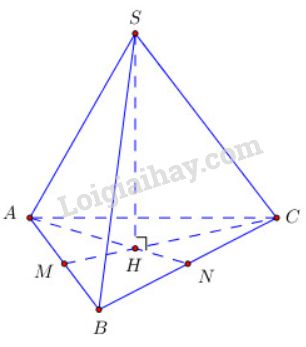
Gọi $H$ là tâm của tam giác đều $ABC$ ta có $SH \, \bot \, (ABC)$

$\Rightarrow d(S,(ABC))=SH$

Gọi $N$ là trung điểm của $BC$ .

$\Rightarrow BN = NC = \dfrac{{3a}}{2}$

Tam giác $ABN$ vuông tại $N$ nên:

$AN = \sqrt {A{B^2} - B{N^2}}$ $= \sqrt {{{\left( {3a} \right)}^2} - {{\left( {\dfrac{{3a}}{2}} \right)}^2}} = \dfrac{{3a\sqrt 3 }}{2}$

$H$ là trọng tâm tam giác $ABC$ $\Rightarrow AH=\dfrac 2 3 .AN = a\sqrt 3$

Áp dụng định lí Pytago vào tam giác vuông $SAH$ ta có:

$SH = \sqrt{SA^{2}-AH^{2}}=\sqrt{4a^{2}-(a\sqrt{3})^{2}}=a.$

Vậy $d\left( {S;\left( {ABC} \right)} \right) = SH = a$ .

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.1 trên 22 phiếu

Bài tiếp theo

Bài 8 trang 120 SGK Hình học 11
Cho tứ diện đều ABCD cạnh a...
Các dạng toán về khoảng cách
Các dạng toán về khoảng cách
Bài 6 trang 119 SGK Hình học 11
Chứng minh rằng nếu đường thẳng nối trung điểm hai cạnh AB và CD...
Bài 5 trang 119 SGK Hình học 11
Cho hình lập phương ABCD.A'B'C'D' cạnh a...
Bài 4 trang 119 SGK Hình học 11
Giải bài 4 trang 119 SGK Hình học 11. Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC= b, CC' = c...
Bài 3 trang 119 SGK Hình học 11
Cho hình lập phương ABCD.A'B'C'D'cạnh a....
Bài 2 trang 119 SGK Hình học 11
Cho tứ diện S.ABC có SA vuông góc với mặt phẳng (ABC). Gọi H, K lần lượt là trực tâm của tam giác ABC và SBC...
Bài 1 trang 119 SGK Hình học 11
Giải bài 1 trang 119 SGK Hình học 11. Trong các mệnh đề sau đây, mệnh đề nào đúng?...
Câu hỏi 6 trang 118 SGK Hình học 11
Giải câu hỏi 6 trang 118 SGK Hình học 11. Chứng minh rằng khoảng cách giữa hai đường thẳng chéo nhau là bé nhất ...
Câu hỏi 5 trang 116 SGK Hình học 11
Cho tứ diện đều ABCD. Gọi M, N lần lượt là trung điểm của cạnh BC và AD. Chứng minh rằng: MN ⊥ BC và MN ⊥ AD (h.3.42)...
Câu hỏi 4 trang 116 SGK Hình học 11
Cho hai mặt phẳng (α) và (β)...
Câu hỏi 3 trang 116 SGK Hình học 11
Cho đường thẳng a song song với mặt phẳng (α)....
Câu hỏi 2 trang 115 SGK Hình học 11
Cho điểm O và mặt phẳng (α). Chứng minh rằng khoảng cách từ điểm O đến mặt phẳng (α) là bé nhất so với các khoảng cách từ O tới một điểm bất kì của mặt phẳng (α).
Câu hỏi 1 trang 115 SGK Hình học 11
Cho điểm O và đường thẳng a. Chứng minh rằng khoảng cách từ điểm O đến đường thẳng a là bé nhất so với các khoảng cách từ O đến một điểm bất kì của đường thẳng a
Lý thuyết khoảng cách
Khoảng cách từ một điểm đến một mặt phẳng, đến một đường thẳng.

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.