-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11
-
HÌNH HỌC - TOÁN 11
-
CHƯƠNG I. PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG TRONG MẶT PHẲNG
-
CHƯƠNG II. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
- Bài 1. Đại cương về đường thẳng và mặt phẳng
- Bài 2. Hai đường thẳng chéo nhau và hai đường thẳng song song
- Bài 3. Đường thẳng và mặt phẳng song song
- Bài 4. Hai mặt phẳng song song
- Bài 5. Phép chiếu song song. Hình biểu diễn của một hình không gian
- Ôn tập chương II - Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
-
CHƯƠNG III. VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
-
ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 11
-
-
Câu hỏi tự luyện Toán 11
-
TẢI 50 ĐỀ KIỂM TRA 15 PHÚT TOÁN 11
-
TẢI 30 ĐỀ KIỂM TRA 1 TIẾT TOÁN 11
-
TẢI 5 ĐỀ THI GIỮA KÌ 1 TOÁN 11
-
TẢI 25 ĐỀ THI HỌC KÌ 1 TOÁN 11
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 11
-
TẢI 20 ĐỀ THI HỌC KÌ 2 TOÁN 11
Bài 6 trang 119 SGK Hình học 11
Chứng minh rằng nếu đường thẳng nối trung điểm hai cạnh AB và CD...
Đề bài
Chứng minh rằng nếu đường thẳng nối trung điểm hai cạnh \(AB\) và \(CD\) của tứ diện \(ABCD\) là đường vuông góc chung của \(AB\) và \(CD\) thì \(AC = BD\) và \(AD = BC\).
Video hướng dẫn giải
Lời giải chi tiết
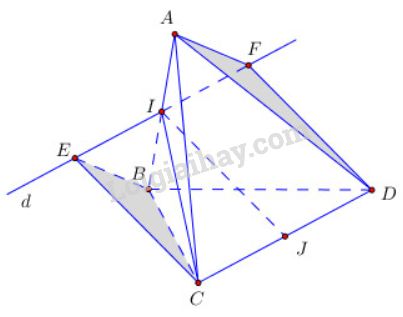
Gọi \(I,J\) lần lượt là trung điểm của \(AB,CD\). Theo giả thiết \(IJ \, \bot \, AB, IJ \, \bot \, CD\).
Qua \(I\) kẻ đường thẳng \(d \, // \, CD\), lấy trên \(d\) điểm \(E, F\) sao cho \(IE = IF = \dfrac{CD}{2}\)
Ta có \(IJ \, \bot \, CD\,\, (gt) \Rightarrow IJ \bot EF\), lại có \(IJ \, \bot \, AB \, \,(gt)\)
\(\Rightarrow IJ \, \bot \, (AEBF)\).
Ta có \(CDFE\) là hình bình hành có \(IJ\) là đường trung bình
\( \Rightarrow CE \, // \, DF \, // \, IJ\)
\( \Rightarrow \left\{ \begin{array}{l}CE \, \bot \, \left( {AEBF} \right) \Rightarrow CE \, \bot \, BE\\DF \, \bot \, \left( {AEBF} \right) \Rightarrow DF \, \bot \, AF\end{array} \right.\)
Ta có: \(\Delta AIF = \Delta BIE(c.g.c)\) suy ra: \(AF=BE\)
Xét \(∆DFA\) và \(∆CEB\) có:
+) \(\widehat E = \widehat F( = {90^0})\)
+) \(AF=BE\)
+) \(DF=CE\)
\(\Rightarrow ∆DFA=∆CEB(c.g.c) \Rightarrow AD = BC\).
Chứng minh tương tự ta được \(BD = AC\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 7 trang 120 SGK Hình học 11
- Bài 8 trang 120 SGK Hình học 11
- Các dạng toán về khoảng cách
- Bài 5 trang 119 SGK Hình học 11
- Bài 4 trang 119 SGK Hình học 11
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Tham Gia Group Dành Cho Lớp 11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
