Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học Bài 1. Vectơ trong không gian

Bài 3 trang 91 SGK Hình học 11


Cho hình bình hành ABCD. Gọi S là một điểm nằm ngoài mặt phẳng...

Đề bài

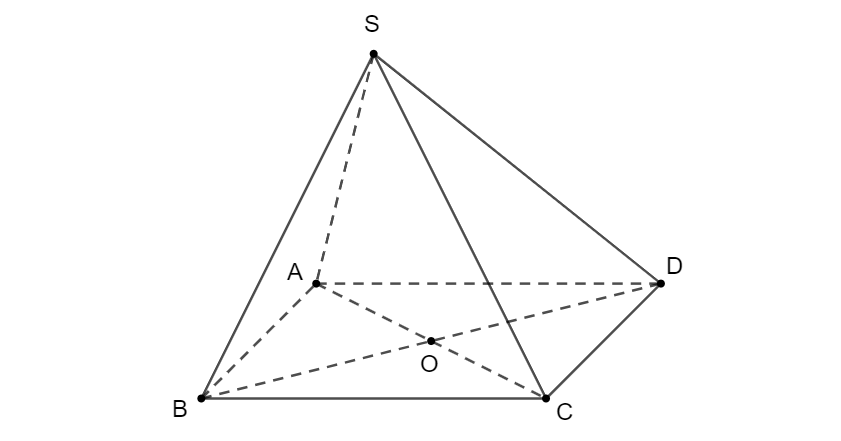
Cho hình bình hành \(ABCD\). Gọi \(S\) là một điểm nằm ngoài mặt phẳng chứa hình bình hành.

Chứng minh rằng: \(\overrightarrow{SA}\) + \(\overrightarrow{SC}\) = \(\overrightarrow{SB}\) + \(\overrightarrow{SD}.\)

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Sử dụng công thức: \(\overrightarrow {MA}  + \overrightarrow {MB}  = 2\overrightarrow {MI} \), với \(M\) là một điểm bất kì trong không gian và \(I\) là trung điểm của \(AB\).

Lời giải chi tiết

Gọi \(O\) là tâm của hình bình hành \(ABCD\), ta có \(O\) là trung điểm của \(AC\) và \(BD\).

Khi đó:

\(\left\{ \matrix{\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} \hfill \cr \overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} \hfill \cr} \right.\)\( \Rightarrow\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD}\,\,\left( {dpcm} \right)\)

 Loigiaihay.com


Bình chọn:
4.4 trên 38 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store