Bài 2 trang 120 Tài liệu dạy – học Toán 9 tập 1

Giải bài tập Trên mặt phẳng tọa độ Oxy, cho đường tròn tâm O bán kính 3

Đề bài

Trên mặt phẳng tọa độ Oxy, cho đường tròn tâm O bán kính 3. Cho các điểm \(A\left( {0;0} \right),B\left( {2;3} \right),C\left( {1;52} \right),D\left( {\sqrt {10} ;2} \right)\). Hãy xác định vị trí các điểm A, B, C, D đối với đường tròn (O).

Phương pháp giải - Xem chi tiết

Cho \(\left( {O;R} \right)\) và điểm \(M\).

+) Nếu \(OM < R \Rightarrow \) M nằm bên tròn \(\left( {O;R} \right)\).

+) Nếu \(OM = R \Rightarrow M\) nằm trên đường tròn \(\left( {O;R} \right)\).

+) Nếu \(OM > R \Rightarrow M\) nằm bên ngoài đường tròn \(\left( {O;R} \right)\).

Lời giải chi tiết

Trước hết, ta chứng minh công thức tính độ dài đoạn thẳng \(OM\) khi biết \(M\left( {{x_M};{y_M}} \right)\) là \(OM = \sqrt {x_M^2 + y_M^2} \).

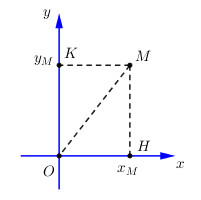
Gọi \(H,\,\,K\) lần lượt là hình chiếu của điểm M trên các trục tọa độ \(Ox,\,\,Oy\) ta có \(OH = \left| {{x_M}} \right|\).

Xét tứ giác \(OHMK\) có \(\widehat {HOK} = \widehat {OHM} = \widehat {OKM} = {90^0} \Rightarrow \) Tứ giác \(OHMK\) là hình chữ nhật (Tứ giác có 3 góc vuông) \( \Rightarrow MH = OK = \left| {{y_M}} \right|\). Có \(OH = \left| {{x_M}} \right|\).

Áp dụng định lý Pytago trong tam giác vuông \(OHM\) có:

\(OM = \sqrt {O{H^2} + M{H^2}} \)\(\, = \sqrt {{{\left| {{x_M}} \right|}^2} + {{\left| {{y_M}} \right|}^2}} = \sqrt {x_M^2 + y_M^2} \)

Áp dụng công thức trên ta có:

\(OA = \sqrt {{0^2} + {0^2}} = 0 < 3 \Rightarrow A\) nằm bên trong \(\left( {O;3} \right)\).

\(OB = \sqrt {{2^2} + {3^2}} = \sqrt {13} > 3 \Rightarrow B\) nằm bên ngoài \(\left( {O;3} \right)\).

\(OC = \sqrt {{1^2} + 5,{2^2}} = \dfrac{{\sqrt {701} }}{5} > 3 \Rightarrow C\) nằm bên ngoài \(\left( {O;3} \right)\).

\(OD = \sqrt {{{\left( {\sqrt {10} } \right)}^2} + {2^2}} = \sqrt {14} > 3 \Rightarrow D\) nằm bên ngoài \(\left( {O;3} \right)\).

Loigiaihay.com