Luyện tập - Chủ đề 5 : Sự xác định đường tròn. Tính chấ..

Bài 1 trang 120 Tài liệu dạy – học Toán 9 tập 1

Giải bài tập Cho tam giác ABC. Vẽ đường tròn (O) đi qua B và C và tâm đường tròn nằm trên AC. Khi nào

Đề bài

Cho tam giác ABC. Vẽ đường tròn (O) đi qua B và C và tâm đường tròn nằm trên AC. Khi nào thì tâm đường tròn (O) trùng với điểm A?

Phương pháp giải - Xem chi tiết

+) Chứng minh điểm \(O\) thuộc trung trực của \(BC\), dựa vào giả thiết suy ra cách dựng điểm \(O\).

+) Chứng minh khi \(O \equiv A\) thì \(A\) thuộc trung trực của \(BC\), từ đó suy ra tính chất của tam giác \(ABC\).

Lời giải chi tiết

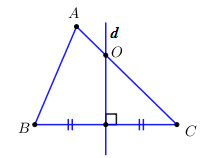
Do \(B,C \in \left( O \right) \Rightarrow OB = OC \Rightarrow \) Điểm \(O\) thuộc trung trực của \(BC\).

Gọi \(d\) là đường trung trực của đoạn thẳng \(BC \Rightarrow O \in d\).

Lại có \(O \in AC\,\,\left( {gt} \right) \Rightarrow O = d \cap AC\).

Khi \(O \equiv A \Rightarrow A \in d \Rightarrow AB = AC\), khi đó tam giác \(ABC\) trở thành tam giác cân tại \(A\).

Vậy điều kiện để \(O \equiv A\) là tam giác \(ABC\) là tam giác cân tại \(A\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài 2 trang 120 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Trên mặt phẳng tọa độ Oxy, cho đường tròn tâm O bán kính 3
Bài 3 trang 120 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Cho hình vuông ABCD.
Bài 4 trang 120 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Cho hình thang cân ABCD ( AB // CD).
Bài 5 trang 120 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Cho tam giác ABC nhọn, hai đường cao BE và CF cắt nhau tại H.

Báo lỗi - Góp ý

Các bài khác cùng chuyên mục

TẢI APP ĐỂ XEM OFFLINE