-
Toán 6 tập 1 - Kết nối tri thức với cuộc sống
-
CHƯƠNG I. TẬP HỢP CÁC SỐ TỰ NHIÊN
- Bài 1. Tập hợp
- Bài 2. Cách ghi số tự nhiên
- Bài 3. Thứ tự trong tập hợp các số tự nhiên
- Bài 4. Phép cộng và phép trừ số tự nhiên
- Bài 5. Phép nhân và phép chia số tự nhiên
- Luyện tập chung trang 20
- Bài 6. Lũy thừa với số mũ tự nhiên
- Bài 7. Thứ tự thực hiện các phép tính
- Luyện tập chung trang 27
- Bài tập cuối chương I
-
CHƯƠNG II. TÍNH CHIA HẾT TRONG TẬP HỢP CÁC SỐ TỰ NHIÊN
-
CHƯƠNG III. SỐ NGUYÊN
-
CHƯƠNG IV. MỘT SỐ HÌNH PHẲNG TRONG THỰC TIỄN
-
CHƯƠNG V.TÍNH ĐỐI XỨNG CỦA HÌNH PHẲNG TRONG TỰ NHIÊN
-
HOẠT ĐỘNG THỰC HÀNH TRẢI NGHIỆM KÌ 1
-
-
Toán 6 tập 2 - Kết nối tri thức với cuộc sống
Lý thuyết Tập hợp các số nguyên Toán 6 KNTT với cuộc sống
Lý thuyết Tập hợp các số nguyên Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu
Tổng hợp đề thi học kì 1 lớp 6 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Khoa học tự nhiên...
1. Làm quen với số nguyên âm
Số nguyên dương: \(1;2;3;4;...\) (Số tự nhiên khác 0)
Số nguyên âm: \(- 1; - 2; - 3; - 4;...\)(Ta thêm dấu “-” vào đằng trước các số nguyên dương)
- Tập hợp: \(\left\{ {...; - 3; - 2; - 1;0;1;2;3;...} \right\}\) gồm các số nguyên âm, số \(0\) và các số nguyên dương là tập hợp các số nguyên. Kí hiệu là \(\mathbb{Z} = \left\{ {...; - 3; - 2; - 1;0;1;2;3;...} \right\}\)
Chú ý:
- Số \(0\) không phải là số nguyên dương cũng không phải số nguyên âm.
- Đôi khi ta còn viết thêm dấu “+” ngay trước một số nguyên dương. Chẳng hạn \( + 5\) (đọc là “dương năm”)
Khi nào người ta dùng số âm?
- Trong đời sống hàng ngày người ta dùng các số mang dấu "-" và dấu "+" để chỉ các đại lượng có thể xét theo hai chiều khác nhau.
|
Số dương biểu thị |
Số âm biểu thị |
|
Nhiệt độ trên \({0^0}C\) |
Nhiệt độ dưới \({0^0}C\) |
|
Độ cao trên mực nước biển |
Độ cao dưới mực nước biển |
|
Số tiền hiện có |
Số tiền còn nợ |
|
Số tiền lãi |
Số tiền lỗ |
|
Độ viễn thị |
Độ cận thị |
Ví dụ:
+) Số \( - 1\) đọc là “âm một”.
+) Số +2 đọc là “dương hai”
+) Một người thợ lặn lặn xuống độ sâu 10 mét tức là độ cao hiện tại của người thợ lặn là -10m so với mực nước biển.
2. Thứ tự trên tập hợp số nguyên
a) Trục số
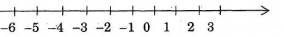
- Chiều dương hướng từ trái sang phải (thường được đánh dấu bằng mũi tên), chiều ngược lại là chiều âm.
- Điểm gốc của trục số là điểm \(0\).
- Điểm biểu diễn số nguyên \(a\) gọi là điểm \(a\).
- Đơn vị đo độ dài trên trục số là độ dài đoạn thẳng nối điểm \(0\) với điểm \(1\).
+) Cho số nguyên \(a\) và \(b\). Trên trục số, nếu điểm \(a\) nằm bên trái điểm \(b\) thì số \(a\) nhỏ hơn số \(b\), kí hiệu \(a < b\)
Ví dụ:
Số 2 trên trục số được gọi là điểm 2.
Số \( - 9\) trên trục số được gọi là điểm \( - 9\)
Ví dụ: Cho trục số như hình vẽ.
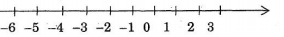
Ta thấy điểm biểu diễ số \( - 5\) nằm bên trái điểm biểu diễn số \( - 3\) nên \( - 5 < - 3.\)
Ngoài ra, ta cũng có thể biểu diễn số nguyên trên trục số thẳng đứng.
b) So sánh hai số nguyên
- Mọi số nguyên âm đều nhỏ hơn 0.
- Mọi số nguyên âm đều nhỏ hơn số nguyên dương.
- Mọi số nguyên dương đều lớn hơn 0.
- Nếu \(a,b\) là hai số nguyên dương và \(a > b\) thì \( - a < - b\) (Thêm dấu “-” thì đổi dấu “>” thành dấu “<”)
- Nếu \(a,b\) là hai số nguyên dương và \(a < b\) thì \( - a > - b\)
- Kí hiệu \(a \le b\) có nghĩa là “\(a < b\) hoặc \(a = b\)”
- Kí hiệu \(a \ge b\) có nghĩa là “\(a > b\) hoặc \(a = b\)”
Chú ý:
+) Để so sánh 2 số nguyên âm, ta làm 2 bước sau:
Bước 1: Bỏ dấu "-" trước cả 2 số âm
Bước 2: Trong 2 số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu( trước khi bỏ dấu "-" lớn hơn
Ví dụ:
5 là số nguyên dương và \( - 25\) là số nguyên âm nên \(5 > - 25\)
Vì \(15 > 3\) nên \( - 15 < - 3\)
Cách nhận biết số nguyên âm:
Số nguyên âm được nhận biết bằng dấu “ – “ ở trước số tự nhiên khác 0.
Ví dụ:
\( - 5\) là số nguyên âm, đọc là: âm năm hoặc trừ năm
Âm hai được viết là: \( - 2\).
3. Ứng dụng thực tiễn
Số nguyên âm được sử dụng trong nhiều tình huống thực tiễn cuộc sống:
- Số nguyên âm được dùng để chỉ nhiệt độ dưới \({0^o}C\).
- Số nguyên âm được dùng để chỉ độ cao dưới mực nước biển.
- Số nguyên âm được dùng để chỉ số tiền nợ, cũng như để chỉ số tiền lỗ trong kinh doanh.
- Số nguyên âm được dùng để chỉ thời gian trước Công nguyên.
Ví dụ:
+ Bác An nợ \(100\,\,000\) đồng thì ta cũng có thể nói bác An có \( - 100\,\,000\) đồng.
+ Một cơ sở kinh doanh bị lỗ \(30\,\,000\,\,000\) đồng thì ta có thể nói lợi nhuận là: \( - 30\,\,000\,\,000\) đồng.
+ Nhà toán học Py-ta-go sinh năm \( - 570\), nghĩa là ông sinh năm \(570\) trước Công nguyên
+ Nhiệt độ 3 độ dưới \({0^o}C\) được viết là \( - {3^o}C\); đọc là: âm ba độ C.
+ Vùng đất trũng dưới mực nước biển \(5\,\,m\), ta nói độ cao trung bình của vùng đất đó là \( - 5\,\,m\).
CÁC DẠNG TOÁN VỀ TẬP HỢP SỐ NGUYÊN
1. Dùng số nguyên để diễn tả các tình huống thực tiễn
- Cách dùng để diễn tả nhiệt độ
+ Số nguyên âm được dùng để chỉ nhiệt độ dưới \({0^o}C\).
+ Số nguyên dương được dùng để chỉ nhiệt độ trên \({0^o}C\).
- Cách dùng để chỉ độ cao so với mực nước biển
+ Số nguyên âm được dùng để chỉ độ cao dưới mực nước biển.
+ Số nguyên dương được dùng để chỉ độ cao trên mực nước biển.
- Cách dùng để chỉ số tiền lãi (lỗ), số tiền nợ
+ Số nguyên âm được dùng để chỉ số tiền nợ, cũng như chỉ số tiền lỗ trong kinh doanh
+ Số nguyên dương được dùng để chỉ số tiền lãi trong kinh doanh.
- Cách dùng để chỉ thời gian trước và sau công nguyên
+ Số nguyên âm được dùng để chỉ thời gian trước công nguyên.
+ Số nguyên dương được dùng để chỉ thời gian sau công nguyên.
2. Tập hợp số nguyên, phân biệt các số thuộc tập hợp số tự nhiên và số nguyên
Phương pháp: Sử dụng định nghĩa các tập hợp số sau đây:
- Tập hợp số tự nhiên: \(\mathbb{N} = \left\{ {0;\,1;\,2;\,3;....} \right\}\)
- Tập hợp số tự nhiên khác 0: \({\mathbb{N}^*} = \left\{ {1;\,2;\,3;\,....} \right\}\)
- Tập hợp số nguyên: \(\mathbb{Z} = \left\{ {...; - 2;\, - 1;\,0;\,\,1;\,\,2;...} \right\}\)
+ Các số nguyên âm: \( - 1;\, - 2;\, - 3;\, - 4;...\)
+ Các số nguyên dương: \(1;\,2;\,3;\,4;\,...\)
Chú ý: Số 0 không là số nguyên âm cũng không là số nguyên dương.
3. Biểu diễn các số nguyên trên trục số
- Trên trục số nằm ngang:
+ Các điểm biểu diễn số nguyên âm nằm ở bên trái gốc 0
+ Các điểm biểu diễn số nguyên dương nằm ở bên phải gốc 0.
- Trên trục số thẳng đứng:
+ Các điểm biểu diễn số nguyên âm nằm ở bên dưới gốc 0
+ Các điểm biểu diễn số nguyên dương nằm ở bên trên gốc 0.
4. Bài toán so sánh hai số nguyên
a) So sánh hai số nguyên trái dấu
Số nguyên âm luôn nhỏ hơn số nguyên dương.
b) So sánh hai số nguyên cùng dấu
Để so sánh hai số nguyên âm, ta làm như sau:
Bước 1: Bỏ dấu “-” trước cả hai số âm.
Bước 2: Trong hai số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu (tương ứng) sẽ lớn hơn.
5. Tìm số nguyên thuộc một khoảng cho trước
Dựa vào qui tắc so sánh các số nguyên để chọn ra các số nguyên thích hợp.
Ví dụ:
Tìm số nguyên \(x\) thỏa mãn: \( - 2 < x \le 1\)
Ta thấy các số nguyên lớn hơn \( - 2\) và nhỏ hơn hoặc bằng \(1\) thỏa mãn đề bài nên:
\(x \in \left\{ { - 1;0;1} \right\}\).
Bình luận
Chia sẻ
- Trả lời Hoạt động 1 trang 58 SGK Toán 6 Kết nối tri thức với cuộc sống
- Trả lời Hoạt động 2 trang 58 SGK Toán 6 Kết nối tri thức với cuộc sống
- Trả lời Luyện tập 1 trang 58 SGK Toán 6 Kết nối tri thức với cuộc sống
- Trả lời Câu hỏi 1 trang 59 SGK Toán 6 Kết nối tri thức với cuộc sống
- Trả lời Vận dụng 1 trang 59 SGK Toán 6 Kết nối tri thức với cuộc sống
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 6 - Kết nối tri thức - Xem ngay
Tham Gia Group Dành Cho 2K13 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
