Bài 4. Lũy thừa với số mũ tự nhiên

Lý thuyết Lũy thừa với số mũ tự nhiên Toán 6 Chân trời sáng tạo

Tải về

Lý thuyết Lũy thừa với số mũ tự nhiên Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu

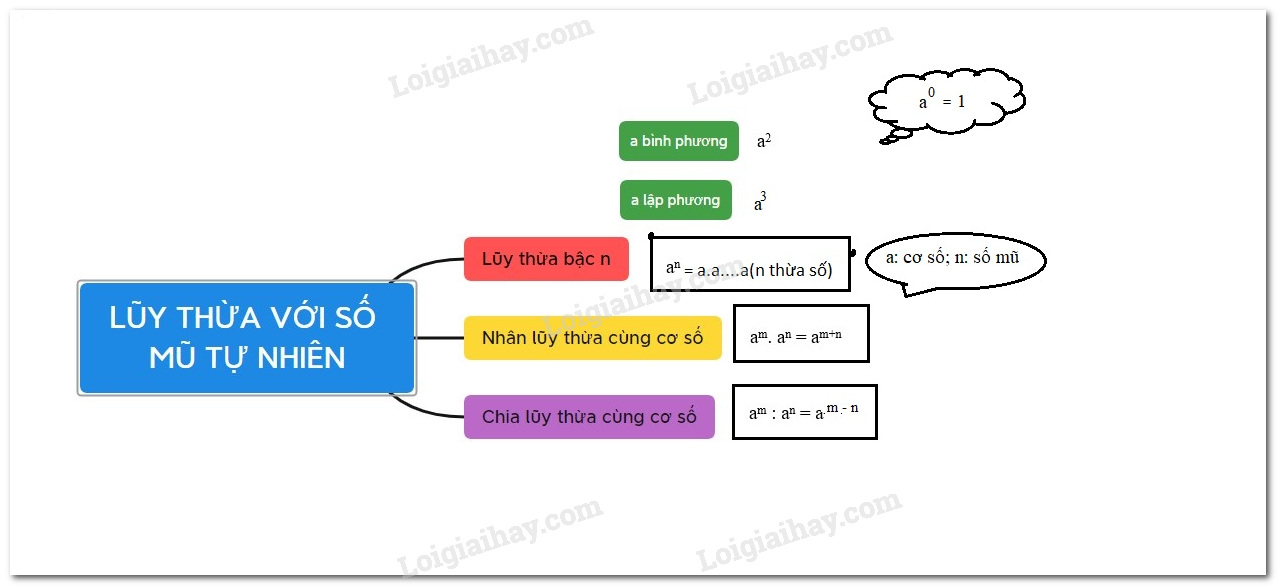
I. Lũy thừa

Lũy thừa với số mũ tự nhiên

Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:

\({a^n} = a.a \ldots ..a\) (\(n\) thừa số \(a\) ) (\(n \notin \mathbb{N}^*\) )

\({a^n}\) đọc là “a mũ n” hoặc “a lũy thừa n”.

\(a\) được gọi là cơ số.

\(n\) được gọi là số mũ.

Phép nhân nhiều thừa số giống nhau như trên được gọi là phép nâng lên lũy thừa.

\({a^1} = a\)

\({a^2} = a.a\) gọi là “\(a\) bình phương” (hay bình phương của \(a\)).

\({a^3} = a.a.a\) gọi là “\(a\) lập phương” (hay lập phương của \(a\)).

Với \(n\) là số tự nhiên khác 0 (thuộc \(\mathbb{N}^*\)), ta có: \({10^n} = 1\underbrace {0...0}_{n{\rm{ \,chữ\, số\, 0}}}\)(số mũ là n thì có n chữ số 0 đằng sau chữ số 1)

Quy ước: \({a^1} = a\); \({a^0} = 1\left( {a \ne 0} \right).\)

Ví dụ:

a) \({8^3}\) đọc là “tám mũ ba”, có cơ số là 8 và số mũ là 3.

b) Tính \({2^3}\).

Số trên là lũy thừa bậc 3 của 2 và là tích của 3 thừa số 2 nhân với nhau nên ta có:

\({2^3} = 2.2.2 = 8\)

c) Tính \({10^3}\)

\({10^3}\) có số mũ là 3 nên \({10^3} = 1000\)(Sau chữ số 1 có 3 chữ số 0).

d) Viết 10 000 000 dưới dạng lũy thừa của 10:

Cách 1: \(10000000 = 10.10.10.10.10.10.10\)\( = {10^7}\)

Cách 2: Sau chữ số 1 có 7 chữ số 0 nên \(10000000 = {10^7}\)

e) Viết 16 dưới dạng lũy thừa cơ số 4:

\(16 = 4.4 = {4^2}\)

II. Nhân hai lũy thừa cùng cơ số

Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.

\({a^m}.{a^n} = {a^{m + n}}\)

Ví dụ:

a) \({3.3^5} = {3^1}{.3^5} = {3^{1 + 5}} = {3^6}.\)

b) \({5^2}{.5^4} = {5^{2 + 4}} = {5^6}\)

c) \({a^3}.{a^5} = {a^{3 + 5}} = {a^8}\)

d) \(x.{x^8} = {x^1}.{x^8} = {x^{1 + 8}} = {x^9}\)

e) \({4^2}.64 = {4^2}.4.4.4 = {4^2}{.4^3} = {4^{2 + 3}} = {4^5}\)

f) \(10.2.5 = 10.\left( {2.5} \right) = 10.10 = {10^2}\) (Sử dụng tính chất kết hợp trong phép nhân trước).

III. Chia hai lũy thừa cùng cơ số

Phép chia hai lũy thừa cùng cơ số

Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ cho nhau.

\({a^m}:{a^n} = {a^{m - n}}\) \(\left( {a \ne 0;\,m \ge n \ge 0} \right)\)

Ví dụ:

a) \({3^5}:3 = {3^5}:{3^1} = {3^{5 - 1}} = {3^4}\)\( = 3.3.3.3 = 81\)

b) \({a^6}:{a^2} = {a^{6 - 2}} = {a^4}\)

c) \({2^3}:{2^3} = {2^{3 - 3}} = {2^0} = 1\)

d) \(81:{3^2} = {3^4}:{3^2} = {3^{4 - 2}} = {3^2} = 3.3 = 9\)

Lưu ý:

Phép chia hai lũy thừa cùng cơ số không thể lấy hai số mũ chia cho nhau mà phải lấy hai số mũ trừ cho nhau.

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 11 phiếu

Tải về

Bài tiếp theo

Trả lời Hoạt động khám phá 1 trang 16 SGK Toán 6 Chân trời sáng tạo
Viết gọn các tích sau bằng cách dùng lũy thừa. a) 5.5.5 b) 7.7.7.7.7.7
Trả lời Thực hành 1 trang 17 SGK Toán 6 Chân trời sáng tạo
a) Viết các tích sau dưới dạng lũy thừa: 3.3.3; 6.6.6.6. b) Phát biểu hoàn thiện các câu sau: 3^2 còn gọi là “3…” hay “…của 3”; 5^3 còn gọi là “5…” hay “…của 5”. c) Hãy đọc các lũy thừa sau và chỉ rõ cơ số, số mũ: 3^10; 10^5
Trả lời Hoạt động khám phá 2 trang 17 SGK Toán 6 Chân trời sáng tạo
Viết tích của hai lũy thừa sau thành một lũy thừa. a) 3.3^3 b) 2^2.2^4.
Trả lời Thực hành 2 trang 17 SGK Toán 6 Chân trời sáng tạo
Viết các tích sau dưới dạng một lũy thừa: 3^3.3^4;,,10^4.10^3;,,x^2. x^5.
Trả lời Hoạt động khám phá 3 trang 17 SGK Toán 6 Chân trời sáng tạo
a) Từ phép tính 5^5.5^2 = 5^7, em hãy suy ra kết quả của mỗi phép tính 5^7:5^2và 5^7:5^5 Giải thích. b) Hãy nhận xét về mối liên hệ giữa số mũ của luỹ thừa vừa tìm được với số mũ của luỹ thừa của số bị chia và số chia trong mỗi phép tính ở trên. Từ nhận xét đó, hãy dự đoán kết quả của mỗi phép tính sau: 7^9:7^2 và 6^5:6^3
Trả lời Thực hành 3 trang 17 SGK Toán 6 Chân trời sáng tạo
a) Viết kết quả mỗi phép tính sau dưới dạng một lũy thừa. 11^7.11^3;,,,,,,,,,,,11^7:11^7;7^2.7^4;,,,,,,,,,,,,,,,,7^2.7^4:7^3 b) Cho biết mỗi phép tính sau đúng hay sai. 9^7:9^2 = 9^5;,,,,,,,,,,,,,,,7^10:7^2 = 7^5;2^11:2^8 = 6;,,,,,,,,,,,,,,,,5^6:5^6= 5
Giải Bài 1 trang 18 SGK Toán 6 Chân trời sáng tạo tập 1
Ghép mỗi phép tính ở cột A với luỹ thừa tương ứng của nó ở cột B.
Giải Bài 2 trang 18 SGK Toán 6 Chân trời sáng tạo
a) Viết kết quả mỗi phép tính sau dưới dạng một luỹ thừa. b) Viết cấu tạo thập phân của các số 4983; 54297; 2023 theo mẫu sau:
Giải Bài 3 trang 18 SGK Toán 6 Chân trời sáng tạo
Theo Tổng cục Thống kê, tháng 10 năm 2020 dân số Việt Nam được làm tròn là 98000000 người. Em hãy viết dân số Việt Nam dưới dạng tích của một số với một luỹ thừa của 10.
Giải Bài 4 trang 18 SGK Toán 6 Chân trời sáng tạo tập 1
Biết rằng khối lượng của Trái Đất khoảng ... a) Em hãy viết khối lượng Trái Đất và khối lượng Mặt Trăng dưới dạng tích của một số với một luỹ thừa của 10. b) Khối lượng Trái Đất gấp bao nhiêu lần khối lượng Mặt Trăng?
Các dạng bài tập về lũy thừa với số mũ tự nhiên
Các dạng bài tập về lũy thừa với số mũ tự nhiên