 Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9
Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9
 Chủ đề 5 : Sự xác định đường tròn. Tính chất đối xứng c..
Chủ đề 5 : Sự xác định đường tròn. Tính chất đối xứng c..
Hoạt động 6 trang 116 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập a) Cho tam giác ABC vuông tại C có O là trung điểm của cạnh huyền AB. Từ O kẻ đường thẳng
Đề bài
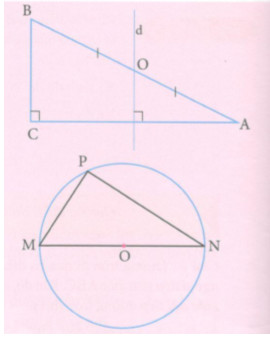
a) Cho tam giác ABC vuông tại C có O là trung điểm của cạnh huyền AB. Từ O kẻ đường thẳng d vuông góc với CA. Chứng minh rằng đường thẳng d là trung trực của đoạn CA. Từ đó suy ra OA = OB = OC.
b) Cho tam giác MNP nội tiếp đường tròn tâm O đường kính MN. Chứng minh rằng
OM = ON = OP. Từ đó suy ra góc MPN vuông.
Lời giải chi tiết
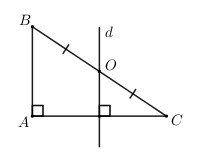
a) Ta có \(\left\{ \begin{array}{l}d \bot AC\\BC \bot AC\end{array} \right. \Rightarrow \) d // BC
Đường thẳng d đi qua trung điểm của AB, song song với BC, do đó áp dụng định lí đường trung bình của tam giác trong tam giác ABC ta có d đi qua trung điểm của CA. Khi đó đường thẳng d vuông góc với AC tại trung điểm của CA.
Vậy d là trung trực của CA.
Mà \(O \in CA \Rightarrow OA = OC\) (điểm thuộc đường trung trực của 1 đoạn thẳng cách đều 2 đầu mút của đoạn thẳng đó). Mà \(OA = OB\,\,\left( {gt} \right)\).
Vậy \(OA = OB = OC\).
b)
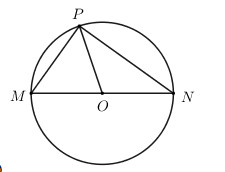
Do M, N, P cùng thuộc đường tròn (O) nên \(OM = ON = OP\).
Tam giác OMP có OM = OP nên tam giác OMP cân tại O \( \Rightarrow \widehat {OMP} = \widehat {OPM}\).
Chứng minh tương tự ta có tam giác OPN cân tại O \(\left( {OP = ON} \right) \Rightarrow \widehat {ONP} = \widehat {OPN}\).
Xét tam giác MNP có \(\widehat {OMP} + \widehat {MPN} + \widehat {ONP} = {180^0}\) (tổng 3 góc trong tam giác)
\(\begin{array}{l} \Rightarrow \widehat {OPM} + \widehat {MPN} + \widehat {OPN} = {180^0}\\ \Rightarrow \left( {\widehat {OPM} + \widehat {OPN}} \right) + \widehat {MPN} = {180^0}\\ \Rightarrow \widehat {MPN} + \widehat {MPN} = {180^0}\\ \Rightarrow 2\widehat {MPN} = {180^0}\\ \Rightarrow \widehat {MPN} = {90^0}\end{array}\)
Vậy tam giác MNP vuông tại P.
Loigiaihay.com












Danh sách bình luận