Hoạt động 3 trang 85 Tài liệu dạy – học Toán 9 tập 2

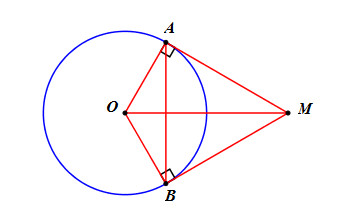
Giải bài tập Trên đường tròn (O) lấy hai điểm A, B. Hai tiếp tuyến tại A và B cắt nhau tại M (xem hình bên).

Đề bài

Trên đường tròn (O) lấy hai điểm A, B. Hai tiếp tuyến tại A và B cắt nhau tại M (xem hình bên). Hãy chứng minh AB vuông góc với OM rồi so sánh các góc \(\widehat {BAM},\widehat {AOM},\widehat {BOM}\).

Lời giải chi tiết

Ta có \(OA = OB = R \Rightarrow O\) thuộc trung trực của AB

\(MA = MB\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow M\) thuộc trung trực của AB.

Từ đó suy ra OM là đường trung trực của AB \( \Rightarrow OM \bot AB\).

Gọi \(H = OM \cap AB\) ta có:

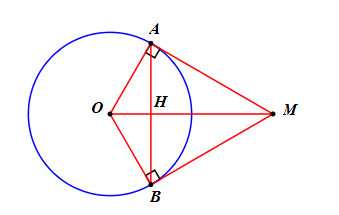
\(\widehat {BAM} + \widehat {AOB} = \widehat {AOM} = {90^0}\) (do AM là tiếp tuyến của (O) nên \(AM \bot OA\))

Tam giác OAH vuông tại H nên \(\widehat {AOM} + \widehat {AOB} = {90^0}\) (hai góc nhọn trong tam giác vuông thì phụ nhau).

\( \Rightarrow \widehat {BAM} = \widehat {AOM}\).

Lại có \(\widehat {AOM} = \widehat {BOM}\) (tính chất hai tiếp tuyến cắt nhau).

Vậy \(\widehat {BAM} = \widehat {AOM} = \widehat {BOM}\) (đpcm).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Hoạt động 4 trang 85 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Vẽ cung lớn AB trên đường tròn (O) và tia tiếp tuyến At tiếp xúc với đường tròn sao cho tâm O
Hoạt động 5 trang 85 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Vẽ đường kính AB và tia tiếp tuyến At của đường tròn (O). So sánh số đo
Bạn nào đúng 3 trang 86 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Hùng nói: “Trên một đường tròn, góc nội tiếp và góc tạo bởi tia tiếp tuyến với dây cung cùng
Thử tài bạn 3 trang 86 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Cho tam giác ABC vuông cân tại A và nội tiếp đường tròn (O). Vẽ tiếp tuyến Au với đường tròn