Bài 5.1 phần bài tập bổ sung trang 119 SBT toán 9 tập 1

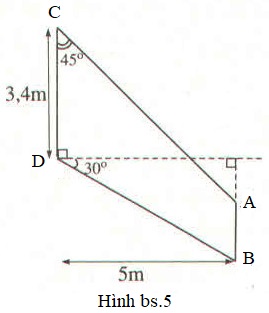
Giải bài 5.1 phần bài tập bổ sung trang 119 sách bài tập toán 9 tập 1. Mô tả cánh của một máy bay.Hãy tính các độ dài AC, BD, AB của cánh máy bay theo số liệu được cho trong hình đó.

Đề bài

(h.bs. 5). Mô tả cánh của một máy bay. Hãy tính các độ dài \(AC,\; BD, \;AB\) của cánh máy bay theo số liệu được cho trong hình đó.

Phương pháp giải - Xem chi tiết

Áp dụng các hệ thức lượng trong tam giác vuông để tìm độ dài các cạnh \(AC,\; BD, \;AB\).

Lời giải chi tiết

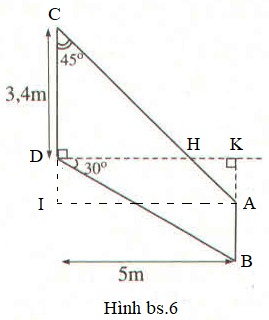
Đường thẳng \(AC\) cắt đường thẳng vuông góc với \(CD\) tại \(D\) ở điểm \(H\) thì tam giác \(CDH\) là tam giác vuông cân (vì là tam giác vuông có góc C bằng \(45^0\)), \(DH = CD = 3,4m\).

Đường thẳng \(AB\) cắt \(DH\) tại \(K\) thì \(DK = 5m\) nên \(H\) nằm ở giữa \(D\) và \(K\) (xem Hình bs.6).

Dựng hình chữ nhật \(AKDI\) thì \(AIC\) là tam giác vuông cân (vì là tam giác vuông có góc C bằng \(45^0\)), \(AI = KD = 5m\)

Xét tam giác vuông AIC ta có: \(AC = \sqrt {A{I^2} + I{C^2}} = \sqrt {{5^2} + {5^2}} = 5\sqrt 2\,(m) \)

Trong tam giác vuông \(BKD\), có:

\(\displaystyle DB = {{DK} \over {\cos 30^\circ }} = {5 \over {\displaystyle {{\sqrt 3 } \over 2}}} = {{10} \over {\sqrt 3 }} \) \(\displaystyle = {{10\sqrt 3 } \over 3} \approx 5,77\,(m)\)

Vì \(DC//AK\) (cùng vuông với DK) nên \(\widehat {KAH} = \widehat C = {45^0}\) (hai góc ở vị trí so le trong)

Suy ra \(HKA\) là tam giác vuông cân (tam giác vuông có góc A bằng \(45^0\))

Do đó: \(AK = HK = DK – DH = DK – DC\) \(= 5 – 3,4 = 1,6m\).

Xét tam giác vuông BDK, ta có: \(KB = DK.tg30^\circ\) \(=5. \dfrac{\sqrt 3 }{3}\) \(= \dfrac{5\sqrt 3 }{3} \).

Suy ra : \(AB = KB – KA\) \( \displaystyle = {{5\sqrt 3 } \over 3} - 1,6 \approx 1,29\,(m)\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 10 phiếu

Bài tiếp theo

Bài 79 trang 119 SBT toán 9 tập 1
Giải bài 79 trang 119 sách bài tập toán 8. Tàu ngầm đang ở trên mặt biển bỗng đột ngột lặn xuống theo phương tạo với mặt nước biển một góc 21^o ....
Bài 78 trang 118 SBT toán 9 tập 1
Giải bài 78 trang 118 sách bài tập toán 9. Một khối u của một căn bệnh nhân cách mặt da 5,7cm được chiếu bởi một chùm tia gamma. Để tránh làm tổn thương mô, bác sĩ đặt nguồn tia cách khối u (trên mặt da) 8,3cm ...
Bài 77 trang 118 SBT toán 9 tập 1
Giải bài 77 trang 118 sách bài tập toán 9. Một máy bay đang bay ở độ cao 10km. Khi bay hạ cánh xuống mặt đất, đường đi của máy bay tạo một góc nghiêng so với mặt đất ...
Bài 76 trang 118 SBT toán 9 tập 1
Giải bài 76 trang 118 sách bài tập toán 9. Một người quan sát ở đài hải đăng cao 80 feet (đơn vị đo lường Anh) so với mặt nước biển, nhìn một chiếc tàu ở xa với góc 0^o 42'...
Bài 75 trang 118 SBT toán 9 tập 1
Giải bài 75 trang 118 sách bài tập toán 9. Đài quan sát ở Toronto, Ontario, Canada cao 533m. Ở một thời điểm nào đó vào ban ngày, Mặt Trời chiếu tạo thành bóng dài 1100m ...
Bài 74 trang 117 SBT toán 9 tập 1
Giải bài 74 trang 117 sách bài tập toán 9. Một con mèo ở trên cành cây cao 6,5m. Để bắt mèo xuống cần phải đặt thang sao cho đầu thang đạt độ cao đó ...
Bài 73 trang 117 SBT toán 9 tập 1
Giải bài 73 trang 117 sách bài tập toán 9. Làm dây kéo cờ : Tìm chiều dài của dây kéo cờ, biết bóng của cột cờ (chiếu bởi ánh sáng mặt trời) dài 11,6m và góc nhìn mặt trời là 36^o 50'.
Bài 72 trang 117 SBT toán 9 tập 1
Giải bài 72 trang 117 sách bài tập toán 9. Thang AB dài 6,7m tựa vào tường làm thành góc 63^o với mặt đất (h.26). Hỏi chiều cao của thang đạt được so với mặt đất ?