Bài 42 trang 107 SBT toán 9 tập 2
Giải bài 42 trang 107 sách bài tập toán 9. Cho ba đường tròn cùng đi qua một điểm P...
Đề bài
Cho ba đường tròn cùng đi qua một điểm \(P.\) Gọi các giao điểm khác \(P\) của hai trong ba đường tròn đó là \(A, B, C.\) Từ một điểm \(D\) (khác điểm \(P\)) trên đường tròn \((PBC)\) kẻ các tia \(DB, DC\) cắt các đường tròn \((PAB)\) và \((PAC)\) lần lượt tại \(M, N.\) Chứng minh ba điểm \(M, A, N\) thẳng hàng.
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \(180^\circ.\)
+) Chứng minh ba điểm thẳng hàng: Nếu \( \widehat{ABD}+\widehat{DBC}=180^\circ\) thì \(A,B,C\) thẳng hàng.
Lời giải chi tiết
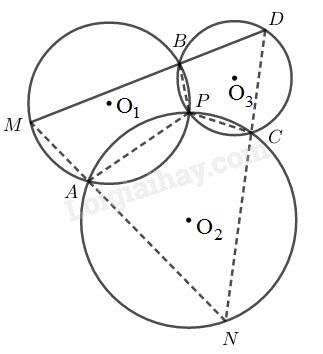
Gọi ba đường tròn tâm \(O_1,O_2,O_3.\)
\((O_1)\) cắt \((O_2)\) tại \(A;\) \((O_1)\) cắt \((O_3)\) tại \(B.\)
\((O_2)\) cắt \((O_3)\) tại \(C.\) Suy ra \(D\) là điểm nằm trên đường tròn \((O_3).\)
\(BD\) cắt \((O_1)\) tại \(M,\) \(DC\) cắt \((O_2)\) tại \(N.\)
Nối \(PA, PB, PC,\) \(MA, NA.\)
Ta có tứ giác \(APBM\) nội tiếp trong đường tròn \((O_1).\)
Nên \(\widehat {MAP} + \widehat {MBP} = 180^\circ \) (tính chất tứ giác nội tiếp)
Mà \(\widehat {MBP} + \widehat {PBD} = 180^\circ \) (hai góc kề bù)
Suy ra: \(\widehat {MAP} = \widehat {PBD}\) \( (1)\)
Ta có: Tứ giác \(APCN\) nội tiếp trong đường tròn \((O_2)\)
Nên \(\widehat {NAP} + \widehat {NCP} = 180^\circ \) (tính chất tứ giác nội tiếp)
Mà \(\widehat {NCP} + \widehat {PCD} = 180^\circ \) (hai góc kề bù)
Suy ra: \(\widehat {NAP} = \widehat {PCD}\) \( (2)\)
Tứ giác \(BPCD\) nội tiếp trong đường tròn \((O_3)\)
\( \Rightarrow \widehat {PBD} + \widehat {PCD} = 180^\circ \) (tính chất tứ giác nội tiếp) \((3)\)
Từ \((1),\) \((2)\) và \((3)\) suy ra: \(\widehat {MAP} + \widehat {NAP} = 180^\circ \)
Vậy ba điểm \(M, A, N\) thẳng hàng.
Loigiaihay.com













Danh sách bình luận