-
ĐẠI SỐ SBT - TOÁN 10
-
HÌNH HỌC SBT - TOÁN 10
-
Chương 1: Véc tơ
-
Chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Bài 1: Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ
- Bài 2: Tích vô hướng của hai vec tơ
- Bài 3: Các hệ thức lượng trong tam giác và giải tam giác
- Ôn tập chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Ôn tập chương 2: Đề toán tổng hợp
- Câu hỏi trắc nghiệm chương 2: Tích vô hướng của hai véc tơ và ứng dụng
-
Chương 3: Phương pháp tọa độ trong mặt phẳng
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Giải SBT toán hình học và đại số 10 cơ bản
Đề toán tổng hợp chương 3: Phương pháp tọa độ trong mặt..
Bài 3.61 trang 168 SBT hình học 10
Giải bài 3.61 trang 168 sách bài tập hình học 10. Trong mặt phẳng tọa độ Oxy, cho đường tròn (C)...
Đề bài
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : \({(x - 1)^2} + {(y - 2)^2} = 4\) và đường thẳng \(d:x - y - 1 = 0\). Viết phương trình đường tròn (C’) đối xứng với đường tròn (C) qua đường thẳng d. Tìm tọa độ các giao điểm của (C’) và (C).
Phương pháp giải - Xem chi tiết
- Tìm tọa độ tâm \(I\) và bán kính \(R\) của đường tròn \(\left( C \right)\).
- Tìm tọa độ điểm \(J\) đối xứng với \(I\) qua \(d\).
- Đường tròn \(\left( {C'} \right)\) đối xứng \(\left( C \right)\) qua \(d\) thì có tâm \(J\) và bán kính \(R\).
- Xét hệ phương trình tọa độ giao điểm của hai đường tròn. Tìm nghiệm và kết luận.
Lời giải chi tiết
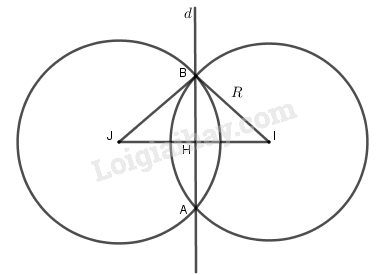
Đường thẳng d có vectơ pháp tuyến là \(\overrightarrow n = \left( {1; - 1} \right).\)
Do đó đường thẳng \(\Delta \) đi qua tâm \(I\left( {1;2} \right)\) và vuông góc với d nên nhận \(\overrightarrow {{u_d}} = \left( {1;1} \right)\) làm VTPT.
\(\Delta\) có phương trình :
\(1\left( {x - 1} \right) + 1\left( {y - 2} \right) = 0\) \( \Leftrightarrow x + y - 3 = 0\)
Tọa độ giao điểm H của d và \(\Delta \) là nghiệm của hệ phương trình :
\(\left\{ \begin{array}{l}x - y - 1 = 0\\x + y - 3 = 0\end{array} \right. \) \(\Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right. \) \(\Rightarrow H\left( {2;1} \right)\)
Gọi J là điểm đối xứng của I qua d. Khi đó:
\(\left\{ \begin{array}{l}{x_J} = 2{x_H} - {x_I} = 3\\{y_J} = 2{y_H} - {y_I} = 0\end{array} \right. \) \(\Rightarrow J(3;0).\)
Vì (C ’) đối xứng với (C ) qua d nên (C ’) có tâm là \(J\left( {3;0} \right)\) và bán kính R = 2.
Do đó (C ’) có phương trình là : \({\left( {x - 3} \right)^2} + {y^2} = 4\)
Tọa độ các giao điểm của (C ) và (C ’) là nghiệm của hệ phương trình :
\(\left\{ \begin{array}{l}{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 4\\{\left( {x - 3} \right)^2} + {y^2} = 4\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x - y - 1 = 0\\{\left( {x - 3} \right)^2} + {y^2} = 4\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}y = x - 1\\2{x^2} - 8x + 6 = 0\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = 1,y = 0\\x = 3,y = 2.\end{array} \right.\)
Vậy tọa độ giao điểm của (C ) và (C ’) là A(1 ; 0) và B(3 ; 2).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 3.62 trang 168 SBT hình học 10
- Bài 3.63 trang 168 SBT hình học 10
- Bài 3.64 trang 168 SBT hình học 10
- Bài 3.60 trang 167 SBT hình học 10
- Bài 3.59 trang 167 SBT hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
