Giải SBT toán hình học và đại số 10 cơ bản

Bài 9 trang 197 Sách bài tập (SBT) Toán Hình học 10

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C)

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : \({(x - 5)^2} + {(y - 3)^2} = 4\). Và điểm A(1 ; 2), một đường thẳng d đi qua A và cắt đường tròn (C) theo một dây cung MN có độ dài bằng \(2\sqrt 3 \). Viết phương trình của d.

Gợi ý làm bài

(Xem hình 3.32)

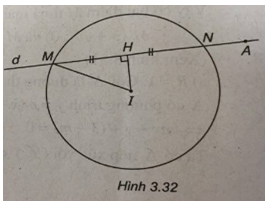
Đường tròn (C) có tâm I(5 ; 3) và có bán kính R = 2.

Gọi H là trung điểm của MN. Ta có

\(IH \bot MN\) và \(MH = {{MN} \over 2} = \sqrt 3 \)

\(IH = \sqrt {I{M^2} - M{H^2}} = \sqrt {4 - 3} = 1.\)

Phương trình đường thẳng d có dạng :

\(y - 2 = k(x - 1) \Leftrightarrow kx - y + 2 - k = 0.\)

Ta có IH = 1

\( \Leftrightarrow {{\left| {5k - 3 + 2 - k} \right|} \over {\sqrt {{k^2} + 1} }} = 1\)

\(\eqalign{
& \Leftrightarrow \left| {4k - 1} \right| = \sqrt {{k^2} + 1} \cr
& \Leftrightarrow {\left( {4k - 1} \right)^2} = {k^2} + 1 \cr} \)

\(\eqalign{
& \Leftrightarrow 15{k^2} - 8k = 0 \cr
& \Leftrightarrow \left[ \matrix{
k = 0 \hfill \cr
k = {8 \over {15}} \hfill \cr} \right. \cr} \)

Vậy có hai điểm d thỏa mãn đề bài.

Đó là \({d_1}:y - 2 = 0\)

\(\eqalign{
& {d_2}:y - 2 = {8 \over {15}}\left( {x - 1} \right) \cr
& \Leftrightarrow 8x - 15y + 22 = 0. \cr} \)

Sachbaitap.net

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục

TẢI APP ĐỂ XEM OFFLINE

Bài giải mới nhất