Bài 25 trang 104 SBT toán 9 tập 2

Giải bài 25 trang 104 sách bài tập toán 9. Từ một điểm M cố định ở bên ngoài đường tròn tâm O ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó...

Đề bài

Từ một điểm \(M\) cố định ở bên ngoài đường tròn tâm \(O\) ta kẻ một tiếp tuyến \(MT\) và một cát tuyến \(MAB\) của đường tròn đó.

\(a)\) Chứng minh rằng ta luôn có \(MT^2= MA.MB\) và tích này không phụ thuộc vị trí của cát tuyến \(MAB.\)

\(b)\) Ở hình \(2\) khi cho \(MB = 20 cm,\)\( MB = 50 cm,\) tính bán kính đường tròn.

Phương pháp giải - Xem chi tiết

Ta sử dụng kiến thức:

+) Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.

+) Hai tam giác đồng dạng thì ta có các cạnh tương ứng tỉ lệ.

Lời giải chi tiết

\(a)\)

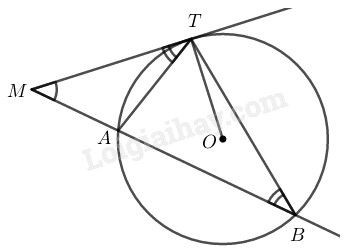
Xét \(∆MTA\) và \(∆MTB,\) có:

+) \(\widehat M\) chung

+) \(\widehat {MTA} = \widehat {TBA}\) (hệ quả góc giữa tia tiếp tuyến và dây), hay \(\widehat {MTA} = \widehat {TBM}\)

Suy ra: \(∆MAT\) đồng dạng \(∆MTB\)

\(\displaystyle \Rightarrow {{MT} \over {MA}} = {{MB} \over {MT}}\)

\( \Rightarrow M{T^2} = MA.MB\)

Vì \(MA.MB=MT^2\) mà \(MT\) là tiếp tuyến của đường tròn \((O)\) nên tích \(MA.MB\) không phụ thuộc vị trí của cát tuyến \(MAB.\)

\(b)\)

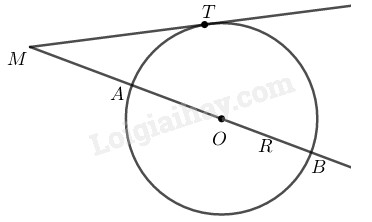
Gọi bán kính \((O)\) là \(R\)

\(MB = MA + AB = MA + 2R\)

\( \Rightarrow MA = MB - 2R\)

\(M{T^2} = MA.MB\) (chứng minh trên)

\( \Rightarrow M{T^2} = \left( {MB - 2R} \right)MB\)

\( \Rightarrow R = \displaystyle {{M{B^2} - M{T^2}} \over {2MB}}\)

\( =\displaystyle {{2500 - 400} \over {2.50}} = 21 (cm)\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4 trên 12 phiếu

Bài 26 trang 104 SBT toán 9 tập 2
Giải bài 26 trang 104 sách bài tập toán 9. Ngồi trên một đỉnh núi cao 1km thì có thể nhìn thấy một địa điểm T trên mặt đất với khoảng cách tối đa là bao nhiêu...
Bài 27 trang 104 SBT toán 9 tập 2
Giải bài 27 trang 104 sách bài tập toán 9. Cho tam giác ABC nội tiếp đường tròn (O). Vẽ tia Bx sao cho tia BC nằm giữa hai tia Bx;...
Bài 4.1 phần bài tập bổ sung trang 104 SBT toán 9 tập 2
Giải bài 4.1 phần bài tập bổ sung trang 104 sách bài tập toán 9. Cho đường tròn tâm O bán kính R. Lấy ba điểm bất kỳ A, B, C trên đường tròn (O)...
Bài 4.2 phần bài tập bổ sung trang 104 SBT toán 9 tập 2
Giải bài 4.1 phần bài tập bổ sung trang 104 sách bài tập toán 9. Cho tam giác ABC vuông ở A, AH và AM tương ứng là đường cao và đường trung tuyến kẻ từ A của tam giác đó. Qua điểm A kẻ đường thẳng...
Bài 24 trang 103 SBT toán 9 tập 2
Giải bài 24 trang 103 sách bài tập toán 9. Hai đường tròn (O) và (O’) cắt nhau tại A và B. Qua A vẽ cát tuyến CAD với hai đường tròn (C (O), D (O’)).