Bài tập 8 trang 141 Tài liệu dạy – học Toán 8 tập 1

Đề bài

Cho tam giác ABC vuông tại A (AB <AC). Gọi D, E, F lần lượt là trung điểm của BC, AB, AC.

a) Chứng minh rằng tứ giác AEDF là hình chữ nhật.

b) Đường thẳng kẻ từ E và song song với BF cắt đường thẳng DF tại N. Chứng minh rằng tứ giác ANCD là hình thoi.

c) Gọi O là giao điểm của AD và EF. Chứng minh rằng ba điểm B, O, N thẳng hàng.

d) Trên tia DN lấy điểm M sao cho N là trung điểm của FM. Qua N kẻ đường thẳng vuông góc với AB cắt MC tại K. Chứng minh ba điểm B, F, K thẳng hàng.

Lời giải chi tiết

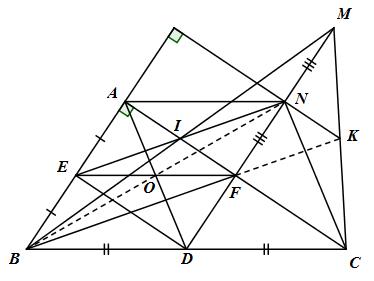
a) E, D lần lượt là trung điểm của AB và BC (gt)

\( \Rightarrow ED\) là đường trung bình của tam giác ABC

\( \Rightarrow ED//AC\) và \(ED = {1 \over 2}AC\).

Tứ giác AEDF có:

ED // AF \(\left( {ED//AC,\,\,F \in AC} \right)\)

Và \(ED = AF\,\,\,\left( { = {1 \over 2}AC} \right)\)

Do đó tứ giác AEDF là hình bình hành

Mà \(\widehat {EAF} = {90^0}\,\,(\Delta ABC\) vuông tại A)

Vậy tứ giác AEDF là hình chữ nhật.

b) Tứ giác BENF có EN // BF (gt)

BE // FN (tứ giác AEDF là hình chữ nhật)

Do đó tứ giác BENF là hình bình hành \( \Rightarrow NF = BE\).

Mà \(EB = EA\) (E là trung điểm của AB)

Và \(FD = EA\) (tứ giác AEDF là hình chữ nhật) nên \(FN = FD\).

Tứ giác ANCD có AC và DN cắt nhau tại F (gt),

F là trung điểm của AC (gt)

F là trung điểm của DN \(\left( {FN = FD,\,\,F \in DN} \right)\)

Do đó tứ giác ANCD là hình bình hành.

Mà \(AC \bot DN\) (tứ giác AEDF là hình chữ nhật)

Vậy tứ giác ANCD là hình thoi (dấu hiệu nhận biết hình thoi)

c) Hình chữ nhật AEDF có AD và EF cắt nhau tại O (gt) \( \Rightarrow O\) là trung điểm của EF.

Tứ giác EBFN là hình bình hành

\( \Rightarrow EF\) và BN cắt nhau tại trung điểm của mỗi đường.

Mà O là trung điểm của EF nên O là trung điểm của BN

Vậy B, O, N thẳng hàng.

d) Ta có \(\left\{ \matrix{  AB = 2AE\,\,\left( {E\,\,là\,\,trung\,\,điểm\,\,của\,AB} \right) \hfill \cr  FM = 2FN\,\,\left( {N\,\,là\,\,trung\,\,điểm\,\,của\,\,FM} \right) \hfill \cr  AE = FN\,\,\left( { = DF} \right) \hfill \cr}  \right.\)

\( \Rightarrow AB = FM\)

Tứ giác ABFM có \(\left\{ \matrix{  AB//FM\,\,\left( {AB//DF,\,\,E \in AB,\,\,M \in DF} \right) \hfill \cr  AB = FM \hfill \cr}  \right.\)

\( \Rightarrow ABFM\) là hình bình hành.

\( \Rightarrow AF\) và BM cắt nhau tại trung điểm của mỗi đường (1)

Tứ giác ANFE có AE // FN \(\left( {AB//DF,\,\,E \in AB,\,\,N \in DF} \right)\)

Và \(AE = FN\,\,\left( { = FD} \right)\)

Do đó tứ giác ANFE là hình bình hành.

Gọi I là giao điểm của AF và EN ta có I là trung điểm của AF (2)

Từ (1) và (2) suy ra I là trung điểm của BM.

Tam giác MFC có NK // FC (cùng vuông góc với AB) và N là trung điểm của FM (gt)

Nên K là trung điểm của MC.ND l

Xét tam giác BMC t có ND và CI cắt nhau tại F (AC cắt DN tại F, \(I \in AC\))

ND là đường trung tuyến (D là trung điểm của BC)

Và CI là đường trung tuyến (I là trung điểm của BM)

Do đó F là trọng tâm của tam giác BMC.

Mặt khác BK là đường trung tuyến của tam giác BMC (K là trung điểm của MC)

Do đó BK đi qua F.

Vậy B, F, K thẳng hàng.

Loigiaihay.com