Bài tập 7 trang 141 Tài liệu dạy – học Toán 8 tập 1

Giải bài tập Cho tam giác ABC vuông tại A ( AB > AC) có AD là đường trung tuyến. E là trung điểm của AC, F là điểm đối xứng của A qua D. G là điểm đối xứng của B qua E.

Đề bài

Cho tam giác ABC vuông tại A ( AB > AC) có AD là đường trung tuyến. E là trung điểm của AC, F là điểm đối xứng của A qua D. G là điểm đối xứng của B qua E.

a) Chứng minh rằng \(DE \bot AC\) .

b) Chứng minh tứ giác ABFC là hình chữ nhật.

c) Đường thẳng qua C song song với AD cắt DE ở H. Chứng minh rằng tứ giác ADCH là hình thoi.

Lời giải chi tiết

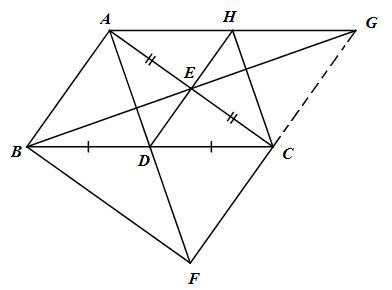
a) D, E lần lượt là trung điểm của BC và AC (gt)

\( \Rightarrow DE\) là đường trung bình của tam giác ABC \( \Rightarrow DE//AB\)

Mà \(AB \bot AC\,\,(\Delta ABC\) vuông tại A) nên \(DE \bot AC\).

b) Tứ giác ABFC có:

BC cắt AF tại D (gt);

D là trung điểm của BC (AD là đường trung tuyến của tam giác ABC)

D là trung điểm của AF (F đối xứng với A qua D)

Do đó tứ giác ABFC là hình bình hành.

Mà \(\widehat {BAC} = {90^0}\,\,(\Delta ABC\) vuông tại A) nên ABFC là hình chữ nhật.

c) Tứ giác ABCG có AC và BG cắt nhau tại E (gt);

E là trung điểm của AC (gt);

E là trung điểm của BG (G đối xứng với B qua E)

Do đó tứ giác ABCG là hình bình hành nên CG // AB

Mà CF // AB (ABFC là hình bình hành)

Do đó CG, CF trùng nhau (Tiên đề Ơ-clit)

Nên G, C, F thẳng hàng \( \Rightarrow C \in FG\).

\(\Delta BGF\) có EC // BF (AC // BF, \(E \in AC\)) và E là trung điểm của BG

\( \Rightarrow C\) là trung điểm của FG.

d) \(\Delta ABC\) vuông tại A có AD là đường trung tuyến (gt) \( \Rightarrow AD = DC = {{BC} \over 2}\)

Tứ giác ADCH có AD // CH (gt) và CD // AH (ABCH là hình bình hành)

Do đó tứ giác ADCH là hình bình hành.

Mà \(AD = DC\) nên tứ giác ADCH là hình thoi.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

2 trên 5 phiếu

Bài tiếp theo

Bài tập 8 trang 141 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho tam giác ABC vuông tại A (AB
Bài tập 6 trang 140 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho tam giác ABC vuông tại A, có AB = 6 cm, AC = 8 cm. Gọi I là trung điểm của BC.
Bài tập 5 trang 140 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho tam giác ABC vuông tại A (AB < AC) có AH là đường cao
Bài tập 4 trang 140 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho tam giác ABC cân tại A. Gọi D, E, H lần lượt là trung điểm của AB, AC, BC.
Bài tập 3 trang 140 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho tam giác ABC vuông tại A (AB < AC). Gọi M là trung điểm của BC.
Bài tập 2 trang 140 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho hình thang ABCD (AB, CD là hai đáy). Gọi M, N, P, Q lần lượt là trung điểmcủa AB, AC, CD, BD.
Bài tập 1 trang 140 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho tam giác ABC (AB < AC). Gọi M, N lần lượt là trung điểm của BC và AC.