-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA ĐA THỨC
-
Chủ đề 1 : Phép nhân đa thức – Hằng đẳng thức đáng nhớ
-
Chủ đề 2 : Phân tích đa thức thành nhân tử
- 1. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- 2. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- 3. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- 4. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
- Luyện tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
-
Chủ đề 3: Phép chia đa thức
-
Ôn tập chương 1 - Phép nhân và phép chia đa thức
-
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
-
CHƯƠNG 1. TỨ GIÁC
-
Chủ đề 1 : Tứ giác – Hình thang
-
Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- 1. Đối xứng trục
- 2. Hình bình hành
- 3. Đối xứng tâm
- 4. Hình chữ nhật
- 5. Tập hợp các điểm cách đều một đường thẳng cho trước
- 6. Hình thoi
- 7. Hình vuông
- Bài tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- Luyện tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
-
Ôn tập chương 1 - Tứ giác
-
-
CHƯƠNG 2. ĐA GIÁC. DIỆN TÍCH ĐA GIÁC
-
CHƯƠNG 3 : PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN – GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH
-
CHƯƠNG 4. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
-
CHƯƠNG 3. TAM GIÁC ĐỒNG DẠNG
-
Chủ đề 1 : Định lí Thales
-
Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- 1. Khái niệm hai tam giác đồng dạng
- 2. Trường hợp đồng dạng thứ nhất (c.c.c)
- 3. Trường hợp đồng dạng thứ hai (c.g.c)
- 4. Trường hợp đồng dạng thứ ba (g.g)
- 5. Các trường hợp đồng dạng của tam giác vuông
- 6. Ứng dụng thực tế của tam giác đồng dạng
- Bài tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- Luyện tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
-
-
CHƯƠNG 4 : HÌNH LĂNG TRỤ ĐỨNG – HÌNH CHÓP ĐỀU
-
ÔN TẬP CUỐI NĂM - TÀI LIỆU DẠY-HỌC TOÁN 8
Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8
Bài tập - Chủ đề 3 : Hình lăng trụ đứng
Bài tập 11 trang 110 Tài liệu dạy – học Toán 8 tập 2
Giải bài tập Tính diện tích xung quanh, diện tích toàn phần của các lăng trụ đứng sau:
Đề bài
Tính diện tích xung quanh, diện tích toàn phần của các lăng trụ đứng sau:
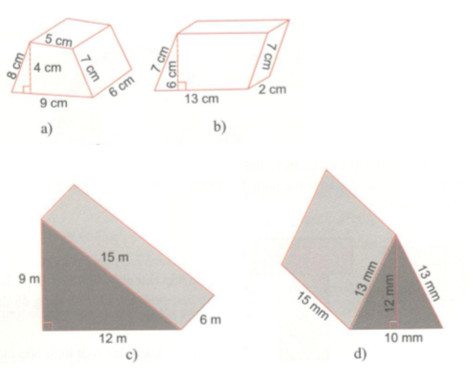
Lời giải chi tiết
a) Hình đã cho là lăng trụ đứng: đáy là hình thang, chiều cao của lăng trụ là 6cm
Diện tích một đáy lăng trụ là: \({S_d} = {1 \over 2}.4.(5 + 9) = 28(c{m^2})\)
Diện tích xung quanh lăng trụ là: \({S_{xq}} = 2p.h = (5 + 7 + 9 + 8).6 = 174(c{m^2})\)
Diện tích toàn phần lăng trụ là: \({S_{tp}} = {S_{xq}} + 2{S_d} = 174 + 2.28 = 230(c{m^2})\)
b) Hình đã cho là lăng trụ đứng: đáy là hình bình hành, chiều cao của lăng trụ là 2cm
Diện tích một đáy lăng trụ là: \({S_d} = 13.6 = 78(c{m^2})\)
Diện tích xung quanh lăng trụ là: \({S_{xq}} = 2p.h = 2.(7 + 13).2 = 80(c{m^2})\)
Diện tích toàn phần lăng trụ là: \({S_{tp}} = {S_{xq}} + 2{S_d} = 80 + 2.78 = 236(c{m^2})\)
c) Hình đã cho là lăng trụ đứng: đáy là tam giác vuông có hai cạnh góc vuông là 9m và 12m, chiều cao của lăng trụ là 6cm
Diện tích một đáy lăng trụ là: \({S_d} = {1 \over 2}.9.12 = 54({m^2})\)
Diện tích xung quanh lăng trụ là: \({S_{xq}} = 2p.h = (9 + 12 + 15).6 = 216({m^2})\)
Diện tích toàn phần lăng trụ là: \({S_{tp}} = {S_{xq}} + 2{S_d} = 216 + 2.54 = 324({m^2})\)
d) Hình đã cho là lăng trụ đứng có đáy là tam giác cân có cạnh đáy là 10mm, chiều cao của lăng trụ là 15mm
Diện tích một mặt đáy lăng trụ là: \({S_d} = {1 \over 2}.12.10 = 60(m{m^2})\)
Diện tích xung quanh lăng trụ là: \({S_{xq}} = 2p.h = (13 + 13 + 10).15 = 540(m{m^2})\)
Diện tích toàn phần lăng trụ là: \({S_{tp}} = {S_{xq}} + 2{S_d} = 540 + 2.60 = 660(m{m^2})\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài tập 10 trang 110 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 12 trang 111 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 13 trang 111 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 14 trang 111 Tài liệu dạy – học Toán 8 tập 2
- Bài tập 15 trang 111 Tài liệu dạy – học Toán 8 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
