Bài 2. Tập hợp số tự nhiên. Ghi số tự nhiên

Lý thuyết Tập hợp số tự nhiên. Ghi số tự nhiên Toán 6 Chân trời sáng tạo

Tải về

Lý thuyết Tập hợp số tự nhiên. Ghi số tự nhiên Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu

Tổng hợp đề thi học kì 1 lớp 6 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Khoa học tự nhiên...

1. Tập hợp N và N*

Các số \(0,1,2,3,4,...\) là các số tự nhiên

Tập hợp các số tự nhiên được kí hiệu là \(\mathbb{N}\), tức là \(\mathbb{N} = \left\{ {0;1;2;3;...} \right\}\)

Tập hợp các số tự nhiên khác 0 được kí hiệu là \({\mathbb{N}^*}\), tức là \({\mathbb{N}^*} = \left\{ {1;2;3;...} \right\}\)

Tập hợp \(\mathbb{N}\) bỏ đi số 0 thì được \({\mathbb{N}^*}\).

Khi cho một số tự nhiên \(x \in {\mathbb{N}^*}\) thì ta hiểu \(x\) là số tự nhiên khác 0.

Ví dụ:

Viết tập hợp sau bằng cách liệt kê các phần tử: \(A = \left\{ {a \in {\mathbb{N}^*}\left| {a < 4} \right.} \right\}\)

\(a \in {\mathbb{N}^*}\) nên \(a\) là các số từ 1;2;3;4;5;6;...

Tuy nhiên thêm điều kiện \(a < 4\) nên \(a\) là các số 1;2;3.

Vậy \(A = \left\{ {1;2;3} \right\}\)

2. So sánh các số tự nhiên

a) Biểu diễn các số tự nhiên trên tia số:

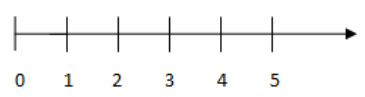
Các số tự nhiên được biểu diễn trên tia số như sau:

+ Tia số có mũi tên sang phải biểu thị chiều tăng dần của các số tự nhiên.

+ Mỗi số tự nhiên được biểu diễn bằng một điểm trên tia số; điểm biểu diễn số tự nhiên n được gọi là điểm n.

+ Điểm 0 được gọi là gốc.

b) So sánh hai số tự nhiên

+ Trong hai số tự nhiên khác nhau, có một số nhỏ hơn số kia, ta viết \(a < b\) ( đọc là \(a\) nhỏ hơn \(b\)) hoặc \(b > a.\) (đọc là \(b\) lớn hơn \(a\))

+ Khi biểu diễn trên tia số nằm ngang có chiều từ trái sang phải, nếu \(a < b\) thì điểm \(a\) nằm bên trái điểm \(b\).

Ngoài ra ta cũng viết \(a \ge b\) để chỉ \(a > b\) hoặc \(a = b.\)

+ Nếu \(a < b\) và \(b < c\) thì \(a < c.\) (Tính chất bắc cầu)

+ Hai số tự nhiên liên tiếp hơn kém nhau 1 đơn vị. Mỗi số tự nhiên có một số liền sau duy nhất và một số liền trước duy nhất.

+ Số 0 là số tự nhiên bé nhất.

Ví dụ:

a) Số 3 và số 4 là hai số tự nhiên liên tiếp.

b) Số liền sau của 89 là 90.

c) Số liền trước của 16 là 15.

3. Ghi số tự nhiên

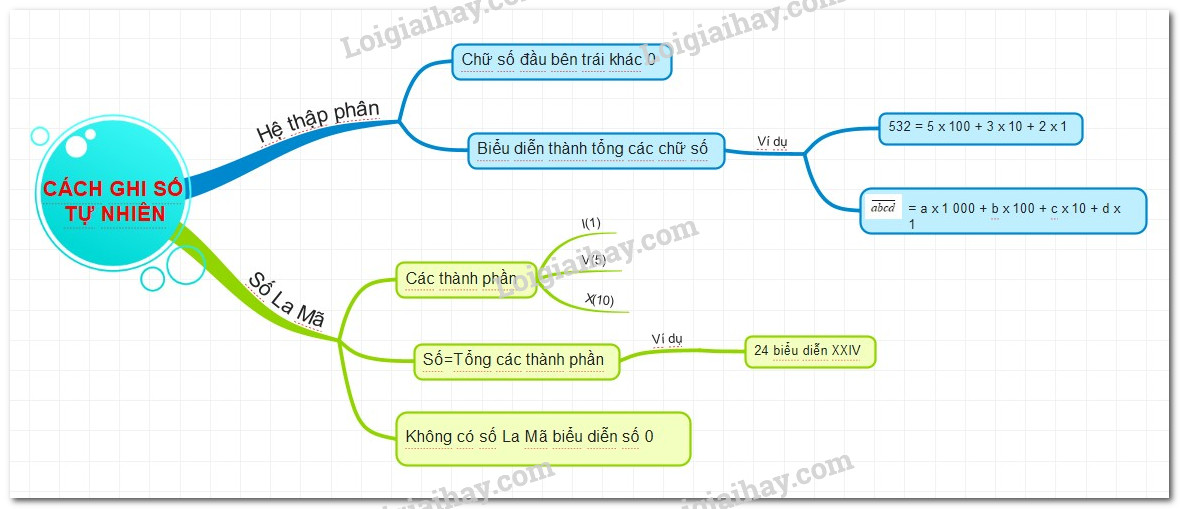
a) Cách ghi số tự nhiên trong hệ thập phân

Để ghi số tự nhiên trong hệ thập phân, người ta dùng mười chữ số là \(0;1;2;3;4;5;6;7;8;9.\) Người ta lấy các chữ số trong 10 chữ số này rồi viết liền nhau thành một dãy, vị trí của các chữ số đó trong dãy gọi là hàng.

Trong hệ thập phân, cứ 10 đơn vị của một hàng thì làm thành 1 đơn vị của hàng liền trước đó. Ví dụ 10 chục thì bằng 1 trăm; mười trăm thì bằng 1 nghìn;...

Chú ý: Khi viết các số tự nhiên, ta quy ước:

1. Với các số tự nhiên khác 0, chữ số đầu tiên bên trái khác 0.

2. Đối với các số có 4 chữ số khác 0 trở lên, ta viết tách riêng từng lớp. Mỗi lớp là một nhóm 3 chữ só từ phải sang trái.

3. Với những số tự nhiên có nhiều chữ số, mỗi chữ số ở các vị trí (hàng) khác nhau thì có giá trị khác nhau

b) Hệ thập phân

Ta đã biết cấu tạo thập phân của một số:

- Kí hiệu \(\overline {ab} \) chỉ số tự nhiên có hai chữ số, chữ số hàng chục là \(a\left( {a \ne 0} \right)\), chữ số hàng đơn vị là b. Ta có:

\(\overline {ab} = a \times 10 + b.\)

Kí hiệu \(\overline {abc} \) chỉ số tự nhiên có ba chữ số, chữ số hàng trăm là \(a\left( {a \ne 0} \right)\), chữ số hàng chục là b, chữ số hàng đơn vị là c. Ta có:

\(\overline {abc} = a \times 100 + b \times 10 + c.\)

- Với các số cụ thể thì không viết dẫu gạch ngang ở trên.

Ví dụ:

\(\begin{array}{l}\overline {2b} = 2.10 + b\\\overline {a5b} = a.100 + 5.10 + b\left( {a \ne 0} \right)\end{array}\)

\(\overline {a03bcd} = a.100000 + 0.10000\)\( + 3.1000 + b.100 + c.10 + d\)\(\left( {a \ne 0} \right)\)

c) Hệ La Mã

Cách ghi số La Mã như sau:

Chữ số	I	V	X
Giá trị tương ứng trong hệ thập phân	1	5	10

Bảng chuyển đổi số La Mã sang số trong hệ thập phân tương ứng (từ 1 đến 10)

Số La Mã	I	II	III	IV	V	VI	VII	VIII	IX	X
Giá trị tương ứng trong hệ thập phân	1	2	3	4	5	6	7	8	9	10

Các số La Mã biểu diễn các số từ 11 đến 20: Thêm X vào bên trái mỗi số từ I đến X

XI	XII	XIII	XIV	XV	XVI	XVII	XVIII	XIX	XX
1	2	3	4	5	6	7	8	9	10

Các số La Mã biểu diễn các số từ 21 đến 30: Thêm XX vào bên trái mỗi số từ I đến X

XXI	XXII	XXIII	XXIV	XXV	XXVI	XXVII	XXVIII	XXIX	XXX
1	2	3	4	5	6	7	8	9	10

Chú ý:

- Mỗi số La Mã biểu diễn một số tự nhiên bằng tổng giá trị của các thành phần tạo nên số đó.

- Không có số La Mã nào biểu diễn số 0.

Ví dụ:

Số XIII có 4 thành phần là X, I, I, I tương ứng với các giá trị 10,1,1,1. Do đó biểu diễn số 10+1+1+1=13.

Viết số 17 thành số La Mã:

Số 7 được viết là VII

Số 17 = 7+10, tức là số 7 thêm 10 đơn vị nên ta thêm chữ X trước VII được: XVII

Bình luận

Chia sẻ

Bình chọn:

4.1 trên 15 phiếu

Tải về

Bài tiếp theo

Trả lời Thực hành 1 trang 10 SGK Toán 6 Chân trời sáng tạo
a) Tập hợp.... b) Viết tập hợp sau bằng cách liệt kê các phần tử: ....
Trả lời Thực hành 2 trang 10 SGK Toán 6 Chân trời sáng tạo
Thay mỗi chữ cái dưới đây bằng một số tự nhiên phù hợp trong những trường hợp sau: a) 17, a, b là ba số lẻ liên tiếp tăng dần; b) m, 101, n, p là bốn số tự nhiên liên tiếp giảm dần.
Trả lời Hoạt động khám phá trang 11 SGK Toán 6 Chân trời sáng tạo
So sánh a và 2020 trong những trường hợp sau: a) a > 2021 b) a < 2000
Trả lời Thực hành 3 trang 11 SGK Toán 6 Chân trời sáng tạo
Cho tập hợp A gồm các số tự nhiên có chữ số tận cùng là 0 hoặc 5 và nhỏ hơn 36. Liệt kê các phần tử của A theo thứ tự giảm dần.
Trả lời Thực hành 4 trang 11 SGK Toán 6 Chân trời sáng tạo
Mỗi số sau có bao nhiêu chữ số? Chỉ ra chữ số hàng đơn vị, hàng chục, hàng trăm, …của mỗi số đó. 2 023; 5 427 198 653
Trả lời Thực hành 5 trang 11 SGK Toán 6 Chân trời sáng tạo
a) Dựa theo cách biểu diễn trên, hãy biểu diễn các số 345 và 2 021. b) Đọc số 96 208 984. Số này có mấy chữ số? Số triệu, số trăm là bao nhiêu?
Trả lời Thực hành 6 trang 12 SGK Toán 6 Chân trời sáng tạo
Hoàn thành bảng sau vào vở...
Giải Bài 1 trang 12 SGK Toán 6 Chân trời sáng tạo tập 1
Chọn kí hiệu thuộc hoặc không thuộc thay cho mỗi dấu ? .
Giải Bài 2 trang 12 SGK Toán 6 Chân trời sáng tạo tập 1
Trong các khẳng định sau, khẳng định nào là đúng, khẳng định nào là sai? a) 1 999 > 2 003 b) 100 000 là số tự nhiên lớn nhất;
Giải Bài 3 trang 12 SGK Toán 6 Chân trời sáng tạo tập 1
Biểu diễn các số 1 983; 2 756; 2 023 theo mẫu 1 983 = 1 x 1 000 + 9 x 100 + 8 x 10 + 3.
Giải Bài 4 trang 12 SGK Toán 6 Chân trời sáng tạo tập 1
Hoàn thành bảng dưới đây vào vở (theo mẫu).
Các dạng toán về tập hợp số tự nhiên, ghi số tự nhiên
Các dạng toán về tập hợp số tự nhiên, ghi số tự nhiên