-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA ĐA THỨC
-
Chủ đề 1 : Phép nhân đa thức – Hằng đẳng thức đáng nhớ
-
Chủ đề 2 : Phân tích đa thức thành nhân tử
- 1. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- 2. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- 3. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- 4. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
- Luyện tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
-
Chủ đề 3: Phép chia đa thức
-
Ôn tập chương 1 - Phép nhân và phép chia đa thức
-
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
-
CHƯƠNG 1. TỨ GIÁC
-
Chủ đề 1 : Tứ giác – Hình thang
-
Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- 1. Đối xứng trục
- 2. Hình bình hành
- 3. Đối xứng tâm
- 4. Hình chữ nhật
- 5. Tập hợp các điểm cách đều một đường thẳng cho trước
- 6. Hình thoi
- 7. Hình vuông
- Bài tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- Luyện tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
-
Ôn tập chương 1 - Tứ giác
-
-
CHƯƠNG 2. ĐA GIÁC. DIỆN TÍCH ĐA GIÁC
-
CHƯƠNG 3 : PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN – GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH
-
CHƯƠNG 4. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
-
CHƯƠNG 3. TAM GIÁC ĐỒNG DẠNG
-
Chủ đề 1 : Định lí Thales
-
Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- 1. Khái niệm hai tam giác đồng dạng
- 2. Trường hợp đồng dạng thứ nhất (c.c.c)
- 3. Trường hợp đồng dạng thứ hai (c.g.c)
- 4. Trường hợp đồng dạng thứ ba (g.g)
- 5. Các trường hợp đồng dạng của tam giác vuông
- 6. Ứng dụng thực tế của tam giác đồng dạng
- Bài tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- Luyện tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
-
-
CHƯƠNG 4 : HÌNH LĂNG TRỤ ĐỨNG – HÌNH CHÓP ĐỀU
-
ÔN TẬP CUỐI NĂM - TÀI LIỆU DẠY-HỌC TOÁN 8
Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8
Luyện tập - Chủ đề 3: Phép chia đa thức
Luyện tập 5 trang 46 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Tìm a, b sao cho đa thức :
Đề bài
Tìm a, b sao cho đa thức : \(3{x^4} - 8{x^3} - 10{x^2} + ax + b\) chia hết cho đa thức \(3{x^2} - 2x + 1\) với mọi x.
Lời giải chi tiết
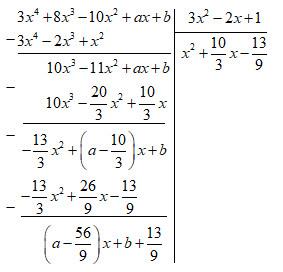
Để đa thức \(3{x^4} - 8{x^3} - 10{x^2} + ax + b\) chia hết cho đa thức \(3{x^2} - 2x + 1\) ta có : \(\left( {a - {{56} \over 9}} \right)x + b + {{13} \over 9} = 0\)
Đẳng thức đúng với mọi x, do đó \(a - {{56} \over 9} = 0\) và \(b + {{13} \over 9} = 0\)
Suy ra \(a = {{56} \over 9}\) và \(b = - {{13} \over 9}\).
Loigiaihay.com
Bình luận
Chia sẻ
- Luyện tập 6 trang 46 Tài liệu dạy – học Toán 8 tập 1
- Luyện tập 7 trang 46 Tài liệu dạy – học Toán 8 tập 1
- Luyện tập 8 trang 46 Tài liệu dạy – học Toán 8 tập 1
- Luyện tập 4 trang 46 Tài liệu dạy – học Toán 8 tập 1
- Luyện tập 3 trang 46 Tài liệu dạy – học Toán 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho Lớp 8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
