Hoạt động 2 trang 123 Tài liệu dạy – học Toán 9 tập 1

Giải bài tập Gọi MN là một dây bất kì của đường tròn (O ; R). Hãy điền vào ô trống :

Đề bài

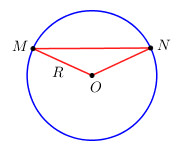
Gọi MN là một dây bất kì của đường tròn (O ; R). Hãy điền vào ô trống :

- Khi MN là đường kính thì MN…2R.

- Khi MN không là đường kính thì MN … 2R.

Vẽ tam giác OMN rồi chứng minh MN < 2R.

Lời giải chi tiết

- Khi \(MN\) là đường kính thì \(MN = 2R\) .

- Khi \(MN\) không là đường kính thì \(MN < 2R\).

Áp dụng bất đẳng thức tam giác đối với tam giác \(OMN\) ta có :

\(MN < OM + ON = R + R = 2R\).

Vậy \(MN < 2R\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Hoạt động 1 trang 123 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Gọi M, N là hai điểm bất kì của đường tròn (O ; R),
Thử tài bạn 1 trang 123 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Cho đường tròn tâm O bán kính 5 cm. A, B là hai điểm bất kì trên đường tròn.
Bạn nào đúng 1 trang 123 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Cho đường tròn (O) và AB, BC, AC là ba dây của đường tròn không phải là đường kính.