-
ĐẠI SỐ SBT - TOÁN 10
-
HÌNH HỌC SBT - TOÁN 10
-
Chương 1: Véc tơ
-
Chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Bài 1: Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ
- Bài 2: Tích vô hướng của hai vec tơ
- Bài 3: Các hệ thức lượng trong tam giác và giải tam giác
- Ôn tập chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Ôn tập chương 2: Đề toán tổng hợp
- Câu hỏi trắc nghiệm chương 2: Tích vô hướng của hai véc tơ và ứng dụng
-
Chương 3: Phương pháp tọa độ trong mặt phẳng
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 2.18 trang 92 SBT hình học 10
Giải bài 2.18 trang 92 sách bài tập hình học 10. Cho tam giác ABC cân (AB = AC)...
Đề bài
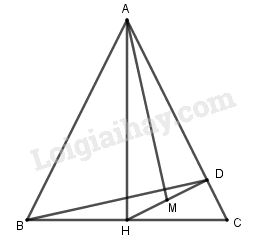
Cho tam giác ABC cân (AB = AC). Gọi H là trung điểm của cạnh BC, D là hình chiếu vuông góc của H trên cạnh AC, M là trung điểm của đoạn HD. Chứng minh rằng AM vuông góc với BD.
Phương pháp giải - Xem chi tiết
Tính tích vô hướng của hai véc tơ \(\overrightarrow {AM} \) và \(\overrightarrow {BD} \) rồi kết luận.
Lời giải chi tiết
Ta cần chứng minh \(\overrightarrow {AM} .\overrightarrow {BD} = 0\)
Ta có: \(2\overrightarrow {AM} = \overrightarrow {AH} + \overrightarrow {AD} \) vì M là trung điểm của đoạn HD.
\(\overrightarrow {BD} = \overrightarrow {BH} + \overrightarrow {HD} \)
Do đó: \(2\overrightarrow {AM} .\overrightarrow {BD} = (\overrightarrow {AH} + \overrightarrow {AD} ).(\overrightarrow {BH} + \overrightarrow {HD} )\)
\( = \underbrace {\overrightarrow {AH} .\overrightarrow {BH} }_{ = 0} + \overrightarrow {AH} .\overrightarrow {HD} + \overrightarrow {AD} .\overrightarrow {BH} + \underbrace {\overrightarrow {AD} .\overrightarrow {HD} }_{ = 0}\)
\( = \overrightarrow {AH} .\overrightarrow {HD} + \overrightarrow {AD} .\overrightarrow {BH} \)
\(\begin{array}{l}
= \overrightarrow {AH} .\overrightarrow {HD} + \left( {\overrightarrow {AH} + \overrightarrow {HD} } \right).\overrightarrow {BH} \\
= \overrightarrow {AH} .\overrightarrow {HD} + \overrightarrow {AH} .\overrightarrow {BH} + \overrightarrow {HD} .\overrightarrow {BH} \\
= \overrightarrow {AH} .\overrightarrow {HD} + \overrightarrow 0 + \overrightarrow {HD} .\overrightarrow {BH} \\
= \overrightarrow {AH} .\overrightarrow {HD} + \overrightarrow {HD} .\overrightarrow {BH} \\
= \overrightarrow {HD} \left( {\overrightarrow {AH} + \overrightarrow {BH} } \right)\\
= \overrightarrow {HD} \left( {\overrightarrow {AH} + \overrightarrow {HC} } \right)\\
= \overrightarrow {HD} .\overrightarrow {AC} \\
= 0
\end{array}\)
Vậy AM vuông góc với BD.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 2.19 trang 92 SBT hình học
- Bài 2.20 trang 92 SBT hình học 10
- Bài 2.21 trang 92 SBT hình học 10
- Bài 2.22 trang 92 SBT hình học 10
- Bài 2.23 trang 92 SBT hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
