Giải SBT toán hình học và đại số 11 nâng cao Bài 2, 3, 4: Hai đường thẳng vuông góc. Đường thẳng vuô..

Câu 24 trang 118 Sách bài tập Hình học 11 Nâng cao


Giải bài tập Câu 24 trang 118 Sách bài tập Hình học 11 Nâng cao

Đề bài

Cho tứ diện ABCD có BC = AD = a, AC = BD = b, AB = CD = c. Đặt α là góc giữa BC và AD; β là góc giữa AC và BD; γ là góc giữa AB và CD. Chứng minh rằng trong ba số hạng \({a^2}\cos \alpha ,{b^2}\cos \beta ,{c^2}\cos \gamma \) có một số hạng bằng tổng hai số hạng còn lại.

Lời giải chi tiết

 

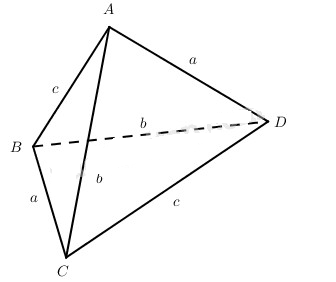
Ta có:

\(\cos \left( {\overrightarrow {BC} ,\overrightarrow {DA} } \right) = {{2{c^2} - 2{b^2}} \over {2{a^2}}} = {{{c^2} - {b^2}} \over {{a^2}}}\).

Vậy nếu góc giữa BC và AD bằng α thì:

\(\cos \alpha  = {{\left| {{c^2} - {b^2}} \right|} \over {{a^2}}}\) hay \({a^2}\cos \alpha  = \left| {{c^2} - {b^2}} \right|\).

Tương tự như trên, nếu gọi β là góc giữa AC và BD thì:

\({b^2}\cos \beta  = \left| {{a^2} - {c^2}} \right|\)

và γ là góc giữa AB và CD thì

\({c^2}\cos \gamma  = \left| {{b^2} - {a^2}} \right|\).

Với a, b, c lần lượt là dộ dài của BC, CA, AB, không giảm tính tổng quát có thể coi a ≥ b ≥ c. Khi đó:

\(\eqalign{  & {a^2}\cos \alpha  = {b^2} - {c^2}  \cr  & {b^2}\cos \beta  = {a^2} - {c^2}  \cr  & {c^2}\cos \gamma  = {a^2} - {b^2} \cr} \).

Từ đó, trong trường hợp này ta có \({b^2}\cos \beta  = {a^2}\cos \alpha  + {c^2}\cos \gamma \).

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store