Giải SBT toán hình học và đại số 11 nâng cao Bài 2, 3, 4: Hai đường thẳng vuông góc. Đường thẳng vuô..

Câu 22 trang 118 Sách bài tập Hình học 11 Nâng cao


Giải bài tập Câu 22 trang 118 Sách bài tập Hình học 11 Nâng cao

Đề bài

Cho hai tam giác cân ABC và DBC có chung cạnh đáy BC và nằm trong hai mặt phẳng khác nhau.

a) Chứng minh rằng AD vuông góc với CB.

b) Gọi M, N là các điểm lần lượt thuộc các đường thẳng AB và DB sao cho \(\overrightarrow {MA}  = k\overrightarrow {MB} ,\overrightarrow {N{\rm{D}}}  = k\overrightarrow {NB} \) . Tính góc giữa hai đường thẳng MN và BC.

Lời giải chi tiết

 

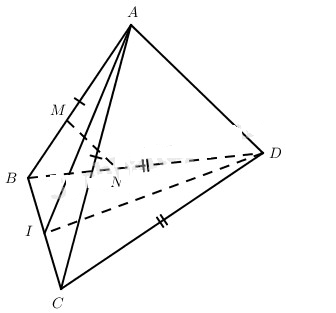
a) Gọi I là trung điểm của BC thì \(AI \bot BC,DI \bot BC\) .

Ta có \(\overrightarrow {A{\rm{D}}}  = \overrightarrow {AI}  + \overrightarrow {I{\rm{D}}} \).

Xét

\(\eqalign{  & \overrightarrow {BC} .\overrightarrow {A{\rm{D}}}  = \overrightarrow {BC} \left( {\overrightarrow {AI}  + \overrightarrow {I{\rm{D}}} } \right)  \cr  &  = \overrightarrow {BC} .\overrightarrow {AI}  + \overrightarrow {BC} .\overrightarrow {I{\rm{D}}}  = 0 \cr} \)

Vậy \(BC \bot A{\rm{D}}\).

b) Từ giả thiết

\(\eqalign{  & \overrightarrow {MA}  = k\overrightarrow {MB}   \cr  & \overrightarrow {N{\rm{D}}}  = k\overrightarrow {NB}  \cr} \)

ta có MN // AD

Vậy góc giữa hai đường thẳng MN và BC bằng góc giữa hai đường thẳng AD và BC. Theo câu a) thì AD vuông góc BC, nên góc giữa MN và BC bằng 90°.

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store