Câu 15 trang 223 Sách bài tập Hình học 11 Nâng cao

Giải bài tập Câu 15 trang 223 Sách bài tập Hình học 11 Nâng cao

Đề bài

Cho hình thang vuông ABCD có \(\widehat A = \widehat D = {90^0}\) , \(AB = 2{\rm{a}},C{\rm{D}} = a,A{\rm{D}} = 3{\rm{a}}\) M là điểm bất kì thuộc đoạn thẳng AD.

a) Xác định vị trí điểm M để hai đường thẳng BM và CM vuông góc với nhau.

b) Gọi S là điểm thuộc đường thẳng vuông góc với mp(ABC) kẻ từ điểm M sao cho SM = AM. Xét mặt phẳng (P) đi qua M và vuông góc với SA. Thiết diện của hình chóp S.ABCD cắt bởi (P) là hình gì? Tính diện tích thiết diện thu được theo a và x, ở đây \(x = AM\left( {0 < x \le 3{\rm{a}}} \right)\).

Lời giải chi tiết

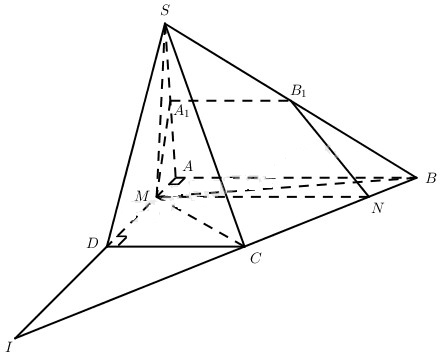
a) Đặt \(AM = x\) thì \(DM=3a-x\).

Dễ thấy \(BC = a\sqrt {10} \)

\(\eqalign{ & M{B^2} = 4{{\rm{a}}^2} + {x^2} \cr & M{C^2} = {a^2} + {\left( {3{\rm{a}} - x} \right)^2} \cr} \)

Hai đường thẳng BM và CM vuông góc với nhau khi và chỉ khi

\(\eqalign{ & B{C^2} = M{B^2} + M{C^2} \cr & \Leftrightarrow 10{a^2} = 2{{\rm{x}}^2} + 14{a^2} - 6ax \cr & \Leftrightarrow {x^2} - 3ax + 2{a^2} = 0 \cr & \Rightarrow x = a,x = 2a \cr} \)

Vậy có hai vị trí của M để MB và MC vuông góc với nhau.

b) Vì \(SM \bot \left( {ABC{\rm{D}}} \right),AB \bot MA\) nên \(AB \bot SA\) (định lí ba đường vuông góc). Mặt khác \(\left( P \right) \bot SA\) nên (P) // AB.

Do MA = MS, (P) đi qua M và \(\left( P \right) \bot SA\) nên (P) cắt SA tại trung điểm A₁ của SA. Từ đó (P) cắt (SAB) theo giao tuyến A₁B₁ với A₁B₁ // AB; (P) cắt (ABCD) theo giao tuyến MN song song với AB. Như vậy, thiết diện của hình chóp S.ABCD khi cắt bởi mp(P) là hình thang vuông M A₁B₁N (tứ giác M A₁B₁N là hình thang vuông MN // A₁B₁, ngoài ta \(AB \bot \left( {SA{\rm{D}}} \right)\) nên \({A_1}{B_1} \bot \left( {SA{\rm{D}}} \right)\), tức là \({A_1}{B_1} \bot M{A_1}\))

\(\eqalign{ & {S_{M{A_1}{B_1}N}} = {1 \over 2}\left( {{A_1}{B_1} + MN} \right).{A_1}M \cr & {A_1}{B_1} = {1 \over 2}AB = a,{A_1}M = {1 \over 2}SA = {{x\sqrt 2 } \over 2} \cr} \)

Gọi I là giao điểm của AD và BC thì IA = 6a. Ta có

\(\eqalign{ & {{MN} \over {AB}} = {{IM} \over {IA}} \Leftrightarrow {{MN} \over {2{\rm{a}}}} = {{6{\rm{a}} - x} \over {6{\rm{a}}}} \cr & \Rightarrow MN = {{6a - x} \over 3} \cr} \)

Vậy

\(\eqalign{ & {S_{M{A_1}{B_1}N}} = {1 \over 2}\left( {a + {{6{\rm{a}} - x} \over 3}} \right).{{x\sqrt 2 } \over 2} \cr & = {{\sqrt 2 \left( {9{\rm{a}} - x} \right)x} \over {12}}\,\left( {voi\,0 < x \le 3{\rm{a}}} \right) \cr} \).

Loigiaihay.com