Giải SBT toán hình học và đại số 11 nâng cao ÔN TẬP CUỐI NĂM - HÌNH HỌC

Câu 6 trang 221 Sách bài tập Hình học 11 Nâng cao


Giải bài tập Câu 6 trang 221 Sách bài tập Hình học 11 Nâng cao

Đề bài

Cho ba điểm A, B, C. Gọi ĐA, ĐB, ĐC là các phép đối xứng tâm có tâm lần lượt là A, B và C. Chứng minh rằng hợp thành của ba phép đối xứng tâm nói trên là một phép đối xứng tâm.

Lời giải chi tiết

 

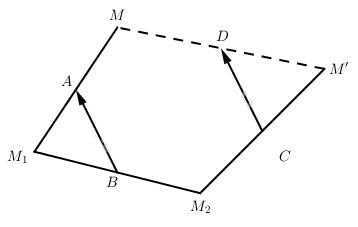
Gọi F là phép hợp thành của ba phép đối xứng ĐA, ĐB và ĐC. Gọi M là điểm bất kì sao cho M1 = ĐA(M), M2 = ĐB(M1), M’ = ĐC(M2), có nghĩa là các điểm A, B, C lần lượt là trung điểm các đoạn \(M{M_1},{M_1}{M_2},{M_2}M'\)

Từ đó nếu ta gọi D là trung điểm của đoạn thẳng MM’ thì \(\overrightarrow {C{\rm{D}}}  = \overrightarrow {BA} \), tức D là điểm xác định không phụ thuộc vào M. Theo định nghĩa của phép hợp thành F thì F biến điểm M thành điểm M’. Vì D là trung điểm của MM’ nên F là phép đối xứng tâm với tâm là D.

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store