Giải SBT toán hình học và đại số 11 nâng cao ÔN TẬP CUỐI NĂM - HÌNH HỌC

Câu 10 trang 222 Sách bài tập Hình học 11 Nâng cao


Giải bài tập Câu 10 trang 222 Sách bài tập Hình học 11 Nâng cao

Đề bài

Cho phép vị tự V có tâm O tỉ số k và phép vị tự V’ có tâm O’ tỉ số k’, biết rằng O, O’ là hai điểm phân biệt và kk’ = 1. Chứng minh rằng hợp thành của V và V’ là một phép tịnh tiến.

Lời giải chi tiết

 

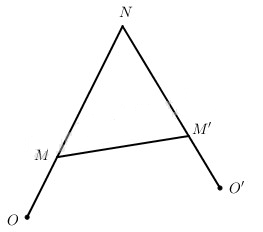
Lấy điểm M tùy ý và giả sử V biến điểm M thành điểm N và V’ biến điểm N thành điểm M’.

Khi đó ta có:

\(\overrightarrow {ON}  = k\overrightarrow {OM} \) và \(\overrightarrow {O'M'}  = k'\overrightarrow {O'N} \). (chú ý rằng kk’ = 1)

Suy ra

\(\eqalign{  & \overrightarrow {OO'}  = \overrightarrow {OM}  + \overrightarrow {MM'}  + \overrightarrow {M'O'}   \cr  &  = {1 \over k}\overrightarrow {ON}  + \overrightarrow {MM'}  - k'\overrightarrow {O'N}   \cr  &  = \overrightarrow {MM'}  + {1 \over k}\left( {\overrightarrow {ON}  + \overrightarrow {NO'} } \right)  \cr  &  = \overrightarrow {MM'}  + {1 \over k}\overrightarrow {OO'}  \cr} \)

Như vậy, ta có \(\overrightarrow {MM'}  = \left( {1 - k} \right)\overrightarrow {OO'} \)               (*)

Vì phéo hợp thành của V và V’ biến M thành M’ nên từ (*) ta suy ra phép hợp thành đó là phép tịnh tiến theo vectơ \(\left( {1 - k'} \right)\overrightarrow {OO'} \).

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store