Bài 5 trang 147 Tài liệu dạy – học Toán 9 tập 1

Đề bài

Cho tam giác ABC nội tiếp đường tròn (O ; R) có AB là đường kính (AC < BC). Đường thẳng song song với AC vẽ từ O cắt đường tròn (O) tại I ( A, C, I, B theo thứ tự).

a) Chứng minh rằng \(OI \bot BC\).

b) Tiếp tuyến với đường tròn (O) tại B cắt đường thẳng OI tại M. Chứng minh rằng MC là tiếp tuyến của (O).

c) Kẻ CH vuông góc với AB tại H, gọi K là giao điểm của AM với CH. Chứng minh rằng K là trung điểm của CH.

Lời giải chi tiết

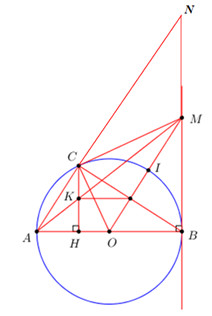
a) Do \(C\) thuộc đường tròn đường kính \(AB \Rightarrow \angle ACB = {90^0} \Rightarrow AC \bot BC\).

Mà \(OI//AC\,\left( {gt} \right) \Rightarrow OI \bot BC\).

b) Vì \(OI//AC\,\,\left( {gt} \right) \Rightarrow \angle MOC = \angle OCA\) (so le trong) ; \(\angle MOB = \angle OAC\)(đồng vị).

Mà \(\Delta OAC\) cân tại \(O\,\,\left( {OA = OC} \right) \Rightarrow \angle OCA = \angle OAC\)

\( \Rightarrow \angle MOC = \angle MOB\)

Xét \(\Delta OMC\) và \(\Delta OMB\) có :

\(\begin{array}{l}OB = OC = R\\\angle MOC = \angle MOB\,\,\left( {cmt} \right)\\OM\,\,chung\\ \Rightarrow \Delta OMC = \Delta OMB\,\,\left( {c.g.c} \right)\\ \Rightarrow \angle OCM = \angle OBM = {90^0}\end{array}\)

\( \Rightarrow MC \bot OC\) tại \(C\). Mà \(OC\) là bán kính của \(\left( O \right)\).

\( \Rightarrow MC\) là tiếp tuyến của \(\left( O \right)\).

c) Kéo dài AN cắt BM tại N.

Ta có \(OI \bot BC\,\,\left( {cmt} \right)\)\( \Rightarrow OM \bot BC\).

Lại có \(AC \bot BC\,\,\left( {cmt} \right) \Rightarrow AC//OM\) hay \(AN//BM\).

Xét tam giác ABN có :

\(O\) là trung điểm của \(AB\).

\(AN//OM\) ;

\( \Rightarrow M\) là trung điểm của \(BN\) (tính chất đường trung bình của tam giác) \( \Rightarrow BM = MN\).

Ta có : \(CH \bot AB;\,\,BN \bot AB \Rightarrow CH//BN\).

Áp dụng định lí Ta-let ta có : \(\dfrac{{KH}}{{BM}} = \dfrac{{AK}}{{AM}} = \dfrac{{KC}}{{MN}}\).

Mà \(BM = MN\,\,\left( {cmt} \right)\) \( \Rightarrow KH = AK\) \( \Rightarrow K\) là trung điểm của \(AH\,\,\left( {dpcm} \right)\).

 Loigiaihay.com