Bài 1 trang 147 Tài liệu dạy – học Toán 9 tập 1

Đề bài

Cho đường tròn (O ; R), đường kính AB = 2R. Lấy điểm C trên đường tròn sao cho CA < CB. Vẽ dây CD vuông góc với AB tại H.

a) Chứng minh rằng tam giác ABC vuông và \(C{D^2} = 4HA.HB\).

b) Đường thẳng (d) tiếp xúc với đường tròn (O) tại C. Gọi M, N lần lượt là hình chiếu vuông góc của A và B trên (d). Xét vị trí tương đối của đường tròn (A ; AM) và đường tròn (B ; BN).

Lời giải chi tiết

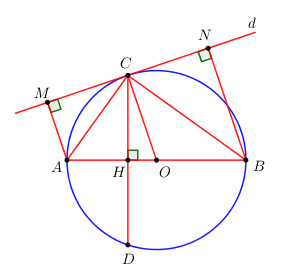
a) Do \(C\) thuộc đường tròn đường kính \(AB \Rightarrow \angle ACB = {90^0}\).

\( \Rightarrow \Delta ABC\) vuông tại \(C\).

 Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) ta có: \(C{H^2} = HA.HB\).

Vì \(AB \bot CD\) tại \(H \Rightarrow H\) là trung điểm của \(CD\) (quan hệ vuông góc giữa đường kính và dây cung)

\( \Rightarrow C{D^2} = {\left( {2CH} \right)^2}\)\(\, = 4C{H^2} = 4HA.HB\) (đpcm).

b) Ta có \(\left\{ \begin{array}{l}AM \bot d\\OC \bot d\end{array} \right. \)

\(\Rightarrow AM//OC \Rightarrow \angle MAC = \angle OCA\) (so le trong).

Lại có \(OA = OC = R \Rightarrow \Delta OAC\) cân tại \(O \Leftrightarrow \angle OCA = \angle OAC\).

\( \Rightarrow \angle MAC = \angle OAC = \angle HAC\).

Xét hai tam giác vuông \(\Delta AMC\) và \({\Delta}AHC\) có :

\(\begin{array}{l}AC\,\,chung\\\angle MAC = \angle HAC\,\,\left( {cmt} \right)\end{array}\)

\( \Rightarrow {\Delta _v}AMC = {\Delta _v}AHC\) (cạnh huyền – góc nhọn) \( \Rightarrow AM = AH\).

Hoàn toàn tương tự ta chứng minh được \({\Delta _v}BNC = {\Delta _v}BHC \Rightarrow BN = BH\).

Xét \(\left( {A;AM} \right)\) và \(\left( {B;BN} \right)\) có \(AM + BN = AH + BH = AB \)

\(\Rightarrow \left( {A;AM} \right)\) và \(\left( {B;BN} \right)\) tiếp xúc ngoài tại \(H\).

 Loigiaihay.com