Bài tập trắc nghiệm Toán 5 có đáp án Bài tập trắc nghiệm Chương 5 Ôn tập

Trắc nghiệm: Ôn tập về phép cộng Toán 5

Đề bài

Xem đáp án

Làm bài tập

Đề bài

Câu 1 :

Cho phép tính ${\rm{a}}\,\,{\rm{ + }}\,\,{\rm{b}}\,\,{\rm{ = }}\,\,{\rm{c}}$.

Con hãy chọn khẳng định sai:

A. $a$ là số hạng

B. $b$ là số hạng

C. $c$ là số hạng

D. $a + b$ là tổng

Câu 2 :

Phép cộng các số tự nhiên, phân số, số thập phân đều có các tính chất nào dưới đây?

A. Tính chất giao hoán

B. Tính chất kết hợp

C. Cộng với $0$

D. Cả A, B, C đều đúng

Câu 3 :

Điền số thích hợp vào ô trống:

$667724 + 69058=$

Câu 4 :

Tính : $\dfrac{3}{7} + \dfrac{5}{{14}}$

A. $\dfrac{8}{{21}}$

B. $\dfrac{{77}}{{14}}$

C. $\dfrac{{11}}{{14}}$

D. $\dfrac{5}{7}$

Câu 5 :

Điền số thích hợp vào ô trống:

$2+\frac{4}{5}=\frac{?}{?}$

Câu 6 :

Điền số thích hợp vào ô trống:

$123,98 + 456,78=$

Câu 7 :

Điền số thích hợp vào ô trống:

Giá trị của biểu thức $34,5 + 18,25 + 47,9$ là

Câu 8 :

Tính giá trị của biểu thức $8,425 + a + b$ với $a = 9,91\,;\,\,b = 24,6$.

A. $42,935$

B. $43,925$

C. $41,915$

D. $40,835$

Câu 9 :

Điền số thích hợp hợp vào ô trống để tính bằng cách thuận tiện:

$\frac{19}{15}+\frac{5}{7}+\frac{11}{15}$

$=(\frac{19}{15}+\frac{?}{?})+\frac{?}{?}$

$=\frac{?}{?}+\frac{?}{?}$

$=?+\frac{?}{?}$

$=\frac{?}{?}$

Câu 10 :

Điền số thích hợp vào ô trống:

Tính bằng cách thuận tiện nhất:

$14,25 + 5,88 + 35,75 + 16,12$

$=\,(14,25 + $

$) \, +\, (5,88\,+ $

$)$

$=$

$+$

$=$

Câu 11 :

Tìm $x$ biết : $x - 16 = 17,98 + 145,2$.

A. $x = 147$

B. $x = 147,18$

C. $x = 179$

D. $x = 179,18$

Câu 12 :

Chọn dấu thích hợp để điền vào chỗ chấm :

$23,24 + 18 + 54,3\; ...\; 37,8 + 57,74$

A. $ = $

B. $ > $

C. $ < $

Câu 13 :

Vòi thứ nhất mỗi giờ chảy được $\dfrac{2}{5}$ thể tích của bể, vòi thứ hai mỗi giờ chảy được $\dfrac{1}{4}$ thể tích của bể. Hỏi cả hai vòi nước cùng chảy vào bể trong một giờ thì được bao nhiêu phần trăm thể tích của bể?

A. $\dfrac{{13}}{{20}}\% $

B. $\dfrac{7}{{20}}\% $

C. $35\% $

D. $65\% $

Câu 14 :

Điền số thích hợp vào ô trống:

Có ba thùng đựng dầu, thùng thứ nhất có $38,5\,$ lít dầu, thùng thứ hai có nhiều hơn thùng thứ nhất $5,75$ lít dầu nhưng ít hơn thùng thứ ba $7,2$ lít dầu.

Vậy ba thùng có tất cả

lít dầu.

Lời giải và đáp án

Câu 1 :

Cho phép tính ${\rm{a}}\,\,{\rm{ + }}\,\,{\rm{b}}\,\,{\rm{ = }}\,\,{\rm{c}}$.

Con hãy chọn khẳng định sai:

A. $a$ là số hạng

B. $b$ là số hạng

C. $c$ là số hạng

D. $a + b$ là tổng

Đáp án

C. $c$ là số hạng

Phương pháp giải :

Dựa vào vị trí của các thành phần trong tổng.

Lời giải chi tiết :

Ta có

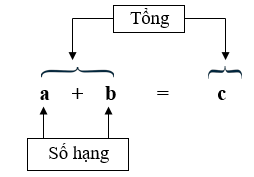
Vậy $c$ là số hạng là khẳng định sai.

Câu 2 :

Phép cộng các số tự nhiên, phân số, số thập phân đều có các tính chất nào dưới đây?

A. Tính chất giao hoán

B. Tính chất kết hợp

C. Cộng với $0$

D. Cả A, B, C đều đúng

Đáp án

D. Cả A, B, C đều đúng

Phương pháp giải :

Dựa vào tính chất của phép cộng các số tự nhiên, phân số, số thập phân.

Lời giải chi tiết :

Phép cộng các số tự nhiên, phân số, số thập phân đều có các tính chất sau:

- Tính chất giao hoán: $a + b = b + a$

- Tính chất kết hợp: $(a + b) + c = a + (b + c)$

- Cộng với $0$: $a + 0 = 0 + a = a$

Vậy cả A, B, C đều đúng.

Câu 3 :

Điền số thích hợp vào ô trống:

$667724 + 69058=$

Đáp án

$667724 + 69058=$

Phương pháp giải :

- Đặt tính theo cột dọc sao cho các số cùng hàng thẳng cột với nhau.

- Cộng nhẩm từng hàng từ phải sang trái, từ hàng đơn vị rồi mới đến các hàng tiếp theo.

Lời giải chi tiết :

Đặt tính rồi thực hiện tính ta có:

$\dfrac{{ + \begin{array}{*{20}{r}}{667724}\\{69058}\end{array}}}{{\,\,\,\,736782}}$

Vậy $667724 + 69058 = 736782$.

Đáp án đúng điền vào ô trống là $736782$.

Câu 4 :

Tính : $\dfrac{3}{7} + \dfrac{5}{{14}}$

A. $\dfrac{8}{{21}}$

B. $\dfrac{{77}}{{14}}$

C. $\dfrac{{11}}{{14}}$

D. $\dfrac{5}{7}$

Đáp án

C. $\dfrac{{11}}{{14}}$

Phương pháp giải :

Quy đồng mẫu số hai phân số đó rồi cộng hai phân số đã quy đồng. Nếu phân số thu được chưa tối giản thì ta rút gọn thành phân số tối giản.

Lời giải chi tiết :

Ta có: $\dfrac{3}{7} + \dfrac{5}{{14}} = \dfrac{6}{{14}} + \dfrac{5}{{14}} = \dfrac{{11}}{{14}}$

Vậy $\dfrac{3}{7} + \dfrac{5}{{14}} = \dfrac{{11}}{{14}}$.

Câu 5 :

Điền số thích hợp vào ô trống:

$2+\frac{4}{5}=\frac{?}{?}$

Đáp án

$2+\frac{4}{5}=\frac{14}{5}$

Phương pháp giải :

Viết $2$ dưới dạng phân số rồi thực hiện phép cộng hai phân số như thông thường. Nếu phân số thu được chưa tối giản thì ta rút gọn thành phân số tối giản.

Lưu ý: số $2$ có thể viết dưới dạng phân số là $\dfrac{2}{1}$.

Lời giải chi tiết :

Ta có: $2 + \dfrac{4}{5} = \dfrac{2}{1} + \dfrac{4}{5} = \dfrac{{10}}{5} + \dfrac{4}{5} = \dfrac{{14}}{5}$

Vậy đáp án đúng điền vào ô trống theo thứ tự từ trên xuống dưới là $14\,;\,\,5$.

Câu 6 :

Điền số thích hợp vào ô trống:

$123,98 + 456,78=$

Đáp án

$123,98 + 456,78=$

Phương pháp giải :

Đặt tính rồi thực hiện tính theo quy tắc:

- Viết số hạng này dưới số hạng kia sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.

- Cộng như cộng các số tự nhiên.

- Viết dấu phẩy ở tổng thẳng cột với các dấu phẩy của các số hạng.

Lời giải chi tiết :

Đặt tính và thực hiện tính ta có:

$\begin{array}{*{20}{c}}{ + \begin{array}{*{20}{c}}{123,98}\\{456,78}\end{array}}\\\hline{\,\,\,\,580,76}\end{array}$

Vậy $123,98 + 456,78= 580,76$.

Số thích hợp điền vào chỗ trống là $580,76$.

Câu 7 :

Điền số thích hợp vào ô trống:

Giá trị của biểu thức $34,5 + 18,25 + 47,9$ là

Đáp án

Giá trị của biểu thức $34,5 + 18,25 + 47,9$ là

Phương pháp giải :

Biểu thức chỉ chứa phép tính cộng nên ta tính lần lượt từ trái sang phải.

Lời giải chi tiết :

$\begin{array}{l}34,5 + 18,25 + 47,9\\ = 52,75 + 47,9\\ = 100,65\end{array}$

Vậy đáp án đúng điền vào ô trống là $100,65$.

Câu 8 :

Tính giá trị của biểu thức $8,425 + a + b$ với $a = 9,91\,;\,\,b = 24,6$.

A. $42,935$

B. $43,925$

C. $41,915$

D. $40,835$

Đáp án

A. $42,935$

Phương pháp giải :

Thay $a = 9,91\,;\,\,b = 24,6$ vào biểu thức $8,425 + a + b$ rồi tính giá trị biểu thức đó.

Biểu thức chỉ chứa phép tính cộng nên ta tính lần lượt từ trái sang phải.

Lời giải chi tiết :

Thay $a = 9,91\,;\,\,b = 24,6$ vào biểu thức $8,425 + a + b$ ta được:

$\begin{array}{l}8,425 + 9,91 + 24,6\\ = 18,335 + 24,6\\ = 42,935\end{array}$.

Vậy giá trị của biểu thức $8,425 + a + b$ với $a = 9,91\,;\,\,b = 24,6$ là $42,935$.

Câu 9 :

Điền số thích hợp hợp vào ô trống để tính bằng cách thuận tiện:

$\frac{19}{15}+\frac{5}{7}+\frac{11}{15}$

$=(\frac{19}{15}+\frac{?}{?})+\frac{?}{?}$

$=\frac{?}{?}+\frac{?}{?}$

$=?+\frac{?}{?}$

$=\frac{?}{?}$

Đáp án

$\frac{19}{15}+\frac{5}{7}+\frac{11}{15}$

$=(\frac{19}{15}+\frac{11}{15})+\frac{5}{7}$

$=\frac{30}{15}+\frac{5}{7}$

$=2+\frac{5}{7}$

$=\frac{19}{7}$

Phương pháp giải :

Áp dụng tính chất giao hoán và kết hợp của phép cộng phân số, gộp cặp phân số có tổng là số tự nhiên lại thành một nhóm.

Lời giải chi tiết :

Ta có:

$\begin{array}{l}\left( {\dfrac{{19}}{{15}} + \dfrac{5}{7}} \right) + \dfrac{{11}}{{15}}\\ = \left( {\dfrac{{19}}{{15}} + \dfrac{{11}}{{15}}\,} \right) + \dfrac{5}{7}\\ = \,\,\,\,\dfrac{{30}}{{15}} + \dfrac{5}{7}\\ = 2 + \dfrac{5}{7}\\ = \dfrac{{19}}{7}\end{array}$

Câu 10 :

Điền số thích hợp vào ô trống:

Tính bằng cách thuận tiện nhất:

$14,25 + 5,88 + 35,75 + 16,12$

$=\,(14,25 + $

$) \, +\, (5,88\,+ $

$)$

$=$

$+$

$=$

Đáp án

Tính bằng cách thuận tiện nhất:

$14,25 + 5,88 + 35,75 + 16,12$

$=\,(14,25 + $

$) \, +\, (5,88\,+ $

$)$

$=$

$+$

$=$

Phương pháp giải :

Áp dụng tính chất giao hoán và kết hợp của phép cộng các số thập phân để nhóm các số thập phân có phần thập phân cộng với nhau thành các số tròn chục, tròn trăm, tròn nghìn, ...

Lời giải chi tiết :

Áp dụng tính chất giao hoán và kết hợp của phép cộng các số thập phân ta có:

$\begin{array}{l}14,25 + 5,88 + 35,75 + 16,12\\ = (14,25 + 35,75) + (5,88 + 16,12)\\ = 50 + 22\\ = 72\end{array}$

Vậy các số cần điền vào lần lượt từ trái sang phải, từ trên xuống dưới là $35,75\,\,;\,\,\,16,12\,\,;\,\,\,50\,\,;\,\,\,22\,\,;\,\,\,72$.

Câu 11 :

Tìm $x$ biết : $x - 16 = 17,98 + 145,2$.

A. $x = 147$

B. $x = 147,18$

C. $x = 179$

D. $x = 179,18$

Đáp án

D. $x = 179,18$

Phương pháp giải :

- Tính giá trị ở vế phải, giá trị này chính là hiệu của phép trừ.

- $x$ ở vị trí số bị chia nên để tìm $x$ ta lấy hiệu cộng với số trừ.

Lời giải chi tiết :

Ta có:

$\begin{array}{l}x - 16 = 17,98 + 145,2\\x - 16 = 163,18\\x = 163,18 + 16\\x = 179,18\end{array}$

Vậy $x = 179,18$.

Câu 12 :

Chọn dấu thích hợp để điền vào chỗ chấm :

$23,24 + 18 + 54,3\; ...\; 37,8 + 57,74$

A. $ = $

B. $ > $

C. $ < $

Đáp án

A. $ = $

Phương pháp giải :

Tính giá trị hai vế rồi so sánh kết quả với nhau.

Lời giải chi tiết :

Ta có:

$\begin{array}{l}23,24 + 18 + 54,3 & & & & 37,8 + 57,74\\ = 41,24 + 54,3 & & & & = \,95,54\\ = 95,54\end{array}$

Mà $95,54 = 95,54$

Vậy $23,24 + 18 + 54,3 = 37,8 + 57,74$.

Câu 13 :

A. $\dfrac{{13}}{{20}}\% $

B. $\dfrac{7}{{20}}\% $

C. $35\% $

D. $65\% $

Đáp án

D. $65\% $

Phương pháp giải :

- Tìm trong một giờ, cả hai vòi nước cùng chảy vào bể được bao nhiêu phần thể tích bể.

- Đổi kết quả dưới dạng phân số sang dạng phần trăm.

Lời giải chi tiết :

Cả hai vòi nước cùng chảy vào bể trong một giờ được số phần thể tích bể là:

$\dfrac{2}{5} + \dfrac{1}{4} = \dfrac{{13}}{{20}}$ (thể tích của bể)

Ta có: $\dfrac{{13}}{{20}} = \dfrac{{65}}{{100}} = 65\% $

Vậy cả hai vòi nước cùng chảy vào bể trong một giờ thì được $65\% $ thể tích của bể.

Câu 14 :

Điền số thích hợp vào ô trống:

Vậy ba thùng có tất cả

lít dầu.

Đáp án

Vậy ba thùng có tất cả

lít dầu.

Phương pháp giải :

- Thùng thứ hai có nhiều hơn thùng thứ nhất $5,75$ lít dầu nên để tính số dầu thùng thứ hai ta lấy số dầu thùng thứ nhất cộng với $5,75$ lít.

- Thùng thứ hai có ít hơn thùng thứ ba $7,2$ lít dầu tức là thùng thứ ba có nhiều hơn thùng thứ hai$7,2$ lít dầu. Để tính số dầu thùng thứ ba ta lấy số dầu thùng thứ hai cộng với $7,2$ lít.

- Để tìm số dầu của cả ba thùng ta lấy số dầu của mỗi thùng cộng lại với nhau.

Lời giải chi tiết :

Thùng thứ hai có số lít dầu là

$38,5\, + 5,75 = 44,25$(lít)

Thùng thứ ba có số lít dầu là

$44,25 + 7,2 = 51,45$ (lít)

Cả ba thùng có số lít dầu là

$38,5\, + 44,25 + 51,45 = 134,2$ (lít)

Đáp số: $134,2$ lít.

Vậy đáp án đúng điền vào ô trống là $134,2$.

Trắc nghiệm: Ôn tập về phép trừ Toán 5

Luyện tập và củng cố kiến thức Ôn tập về phép trừ Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Ôn tập về phép nhân Toán 5

Luyện tập và củng cố kiến thức Ôn tập về phép nhân Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Ôn tập về phép chia Toán 5

Luyện tập và củng cố kiến thức Ôn tập về phép chia Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Ôn tập các phép tính với số đo thời gian Toán 5

Luyện tập và củng cố kiến thức Ôn tập các phép tính với số đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Ôn tập về hình học: Tính chu vi, diện tích một số hình Toán 5

Luyện tập và củng cố kiến thức Ôn tập về hình học: Tính chu vi, diện tích một số hình Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Ôn tập về hình học: Tính diện tích, thể tích một số hình Toán 5

Luyện tập và củng cố kiến thức Ôn tập về hình học: Tính diện tích, thể tích một số hình Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Ôn tập về số đo thời gian Toán 5

Luyện tập và củng cố kiến thức Ôn tập về số đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Ôn tập về đo diện tích và đo thể tích Toán 5

Luyện tập và củng cố kiến thức Ôn tập về đo diện tích và đo thể tích Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Ôn tập về đo độ dài và đo khối lượng Toán 5

Luyện tập và củng cố kiến thức Ôn tập về đo độ dài và đo khối lượng Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Ôn tập về số thập phân Toán 5

Luyện tập và củng cố kiến thức Ôn tập về số thập phân Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Ôn tập về phân số Toán 5

Luyện tập và củng cố kiến thức Ôn tập về phân số Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Ôn tập về số tự nhiên Toán 5

Luyện tập và củng cố kiến thức Ôn tập về số tự nhiên Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Bài giải mới nhất

Trắc nghiệm: Ôn tập về phép cộng Toán 5

Báo lỗi góp ý