Bài tập trắc nghiệm Toán 5 có đáp án Bài tập trắc nghiệm Chương 1 Ôn tâp và bổ sung về phân ..

Trắc nghiệm: Ôn tập về giải toán Toán 5

Đề bài

Xem đáp án

Làm bài tập

Đề bài

Câu 1 :

Khi biết tổng và hiệu của hai số, ta có thể áp dụng công thức nào để tìm hai số đó?

A. Số lớn = (tổng + hiệu) : $2$

B. Số bé = (tổng – hiệu) : $2$

C. Cả A và B đều sai

D. Cả A và B đều đúng

Câu 2 :

Điền số thích hợp vào ô trống:

Cho hai số có tổng là $128$ và hiệu hai số là $54$.

Vậy số lớn là

, số bé là

Câu 3 :

Lớp 5A có tất cả 45 học sinh. Biết số học sinh nữ bằng $\dfrac{4}{5}$ số học sinh nam. Hỏi lớp 5A có bao nhiêu học sinh nam, bao nhiêu học sinh nữ?

A. $33$ học sinh nam; $12$ học sinh nữ

B. $25$ học sinh nam; $20$ học sinh nữ

C. $20$ học sinh nam; $25$ học sinh nữ

D. $30$ học sinh nam; $15$ học sinh nữ

Câu 4 :

Điền số thích hợp vào ô trống.

Tấm vải thứ nhất dài hơn tấm vải thứ hai $72m$, biết tấm vải thứ nhất dài gấp $5$ lần tấm vải thứ hai.

Vậy tấm vải thứ nhất dài

mét.

Tấm vải thứ hai dài

mét.

Câu 5 :

Một hình chữ nhật có chu vi là $112cm$. Biết chiều rộng bằng $\dfrac{3}{4}$ chiều dài. Tính diện tích hình chữ nhật đó.

A. $768c{m^2}$

B. $1536c{m^2}$

C. $2304c{m^2}$

D. $3072c{m^2}$

Câu 6 :

Điền số thích hợp vào chỗ trống:

Hiệu của hai số là $57$, nếu giảm số lớn đi $4$ lần thì ta được số bé. Vậy tổng của hai số đó là

Câu 7 :

Một người có $3$ tạ gạo tẻ và gạo nếp. Sau khi người đó bán đi $65kg$ gạo tẻ và $30kg$ gạo nếp thì còn lại số gạo nếp bằng $\dfrac{1}{4}$ số gạo tẻ. Hỏi lúc đầu người đó có bao nhiêu ki-lô-gam gạo mỗi loại?

A. $259kg$ gạo tẻ; $41kg$ gạo nếp

B. $229kg$ gạo tẻ; $71kg$ gạo nếp

C. $225kg$ gạo tẻ; $75kg$ gạo nếp

D. $400kg$ gạo tẻ; $100kg$ gạo nếp

Câu 8 :

Điền số thích hợp vào ô trống:

Đàn gà nhà An có một số con gà trống và gà mái, trong đó có $48$ con gà trống và số gà mái bằng $\dfrac{2}{5}$ số gà của cả đàn.

Vậy nhà An nuôi được

con gà mái.

Câu 9 :

Điền số thích hợp vào ô trống:

Tổng của hai số là $374$. Nếu viết thêm chữ số $0$ vào bên phải số bé thì được số lớn.

Vậy số bé là

Số lớn là

Câu 10 :

Hai năm trước tuổi mẹ gấp $8$ lần tuổi con. Sau ba năm nữa tổng số tuổi của hai mẹ con là $46$ tuổi. Hỏi năm nay mẹ bao nhiêu tuổi, con bao nhiêu tuổi?

A. Con $4$ tuổi; mẹ $32$ tuổi

B. Con $6$ tuổi; mẹ $34$ tuổi

C. Con $7$ tuổi; mẹ $35$ tuổi

D. Con $9$ tuổi; mẹ $37$ tuổi

Lời giải và đáp án

Câu 1 :

Khi biết tổng và hiệu của hai số, ta có thể áp dụng công thức nào để tìm hai số đó?

A. Số lớn = (tổng + hiệu) : $2$

B. Số bé = (tổng – hiệu) : $2$

C. Cả A và B đều sai

D. Cả A và B đều đúng

Đáp án

D. Cả A và B đều đúng

Phương pháp giải :

Dựa vào công thức tìm hai số khi biết tổng và hiệu của hai số đó.

Lời giải chi tiết :

Với dạng toán tìm hai số khi biết tổng và hiệu của $2$ số, để tìm hai số ta có thể áp dụng công thức sau:

Số bé = (tổng – hiệu) : $2$

Số lớn = (tổng + hiệu) : $2$

Vậy cả hai đáp án A và B đều đúng.

Câu 2 :

Điền số thích hợp vào ô trống:

Cho hai số có tổng là $128$ và hiệu hai số là $54$.

Vậy số lớn là

, số bé là

Đáp án

Cho hai số có tổng là $128$ và hiệu hai số là $54$.

Vậy số lớn là

, số bé là

Phương pháp giải :

Đây là dạng toán tìm hai số khi biết tổng và hiệu của $2$ số đó.

Để tìm hai số ta áp dụng công thức sau:

Số bé = (tổng – hiệu) : $2$;

Số lớn = (tổng + hiệu) : $2$.

Lời giải chi tiết :

Ta có sơ đồ:

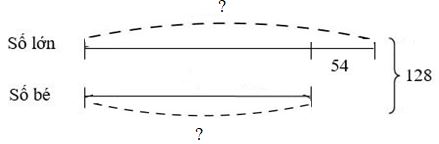
Số lớn là : $(128 + 54):\,2 = 91$

Số bé là: $128 - 91 = 37$

Đáp số: Số bé: $37$;

Số lớn: $91$.

Vậy hai số điền vào ô trống theo thứ tự là $91;\,37$.

Câu 3 :

Lớp 5A có tất cả 45 học sinh. Biết số học sinh nữ bằng $\dfrac{4}{5}$ số học sinh nam. Hỏi lớp 5A có bao nhiêu học sinh nam, bao nhiêu học sinh nữ?

A. $33$ học sinh nam; $12$ học sinh nữ

B. $25$ học sinh nam; $20$ học sinh nữ

C. $20$ học sinh nam; $25$ học sinh nữ

D. $30$ học sinh nam; $15$ học sinh nữ

Đáp án

B. $25$ học sinh nam; $20$ học sinh nữ

Phương pháp giải :

Bài toán cho biết tổng số học sinh và tỉ số của học sinh nữ so với học sinh nam.

Đây là dạng toán tìm hai số khi biết tổng và tỉ số của 2 số đó.

Theo bài ra số học sinh nữ bằng $\dfrac{4}{5}$ số học sinh nam nên ta vẽ sơ đồ biểu thị số học sinh nữ gồm $4$ phần, số học sinh gồm $5$ phần như thế. Coi số học sinh nữ là số bé, số học sinh nam là số lớn, ta tìm hai số theo công thức:

Số bé = Giá trị một phần × số phần của số bé

hoặc

Số lớn = Giá trị một phần × số phần của số lớn

Lời giải chi tiết :

Ta có sơ đồ:

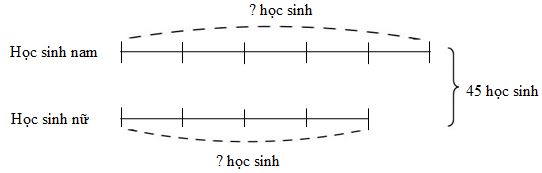
Theo sơ đồ, tổng số phần bằng nhau là:

$4 + 5 = 9$ (phần)

Giá trị một phần là:

$45:9 = 5$ (học sinh)

Lớp 5A có số học sinh nữ là:

$5 \times 4 = 20$ (học sinh)

Lớp 5A có số học sinh nam là:

$45 - 20 = 25$ (học sinh)

Đáp số: $25$ học sinh nam;

$20$ học sinh nữ.

Câu 4 :

Điền số thích hợp vào ô trống.

Tấm vải thứ nhất dài hơn tấm vải thứ hai $72m$, biết tấm vải thứ nhất dài gấp $5$ lần tấm vải thứ hai.

Vậy tấm vải thứ nhất dài

mét.

Tấm vải thứ hai dài

mét.

Đáp án

Vậy tấm vải thứ nhất dài

mét.

Tấm vải thứ hai dài

mét.

Phương pháp giải :

Bài toán cho biết hiệu độ dài hai tấm vải và tỉ số của hai tấm vải.

Đây là dạng toán tìm hai số khi biết hiệu và tỉ số của 2 số đó.

+ Theo bài ra tấm vải thứ nhất dài gấp $5$ lần tấm vải thứ hai nên ta vẽ sơ đồ biểu thị tấm vải thứ hai gồm $1$ phần, tấm vải thứ nhất gồm $5$ phần như thế. Cọi tấm vải thứ hai là số bé, tấm vải thứ nhất là số lớn, ta tìm hai số theo công thức:

Số bé = Giá trị một phần × số phần của số bé

hoặc

Số lớn = Giá trị một phần × số phần của số lớn.

Lời giải chi tiết :

Ta có sơ đồ:

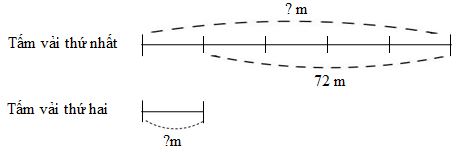
Theo sơ đồ, hiệu số phần bằng nhau là:

$5 - 1 = 4$ (phần)

Giá trị một phần là:

$72:4 = 18\,(m)$

Tấm vải thứ hai dài số mét là:

$18 \times 1 = 18\,(m)$

Tấm vải thứ nhất dài số mét là:

$18 + 72 = 90\,(m)$

Đáp số: Tấm vải thứ nhất: $90m$;

Tấm vải thứ hai: $18m$.

Câu 5 :

Một hình chữ nhật có chu vi là $112cm$. Biết chiều rộng bằng $\dfrac{3}{4}$ chiều dài. Tính diện tích hình chữ nhật đó.

A. $768c{m^2}$

B. $1536c{m^2}$

C. $2304c{m^2}$

D. $3072c{m^2}$

Đáp án

A. $768c{m^2}$

Phương pháp giải :

- Bài toán cho chu vi hình chữ nhật và yêu cầu tìm diện tích. Để tìm được diện tích hình chữ nhật ta phải tìm được chiều dài và chiều rộng hình chữ nhật đó.

- Có chu vi hình chữ nhật ta tìm được nửa chu vi, tức là tìm được tổng của chiều dài và chiều rộng. Từ đây ta đưa được về bài toán dạng tìm hai số khi biết tổng và tỉ số của hai số.

Theo bài ra chiều rộng bằng $\dfrac{3}{4}$ chiều dài nên ta vẽ sơ đồ biểu thị chiều rộng gồm $3$ phần, chiều dài gồm $4$ phần như thế. Cọi chiều rộng là số bé, chiều dài là số lớn, ta tìm hai số theo công thức:

Số bé = Giá trị một phần × số phần của số bé

hoặc

Số lớn = Giá trị một phần × số phần của số lớn.

Lời giải chi tiết :

Nửa chu vi hình chữ nhật đó là:

$112:2 = 56\,(cm)$

Ta có sơ đồ:

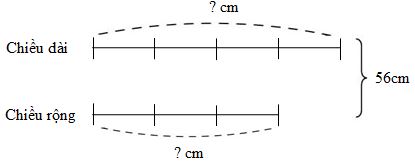
Theo sơ đồ, tổng số phần bằng nhau là:

$4 + 3 = 7$ (phần)

Giá trị một phần là:

$56:7 = 8\,(cm)$

Chiều dài hình chữ nhật đó là:

$8 \times 4 = 32\,(cm)$

Chiều rộng hình chữ nhật đó là:

$56 - 32 = 24\,(cm)$

Diện tích hình chữ nhật đó là:

$32 \times 24 = 768\,(c{m^2})$

Đáp số: $768c{m^2}$

Câu 6 :

Điền số thích hợp vào chỗ trống:

Hiệu của hai số là $57$, nếu giảm số lớn đi $4$ lần thì ta được số bé. Vậy tổng của hai số đó là

Đáp án

Hiệu của hai số là $57$, nếu giảm số lớn đi $4$ lần thì ta được số bé. Vậy tổng của hai số đó là

Phương pháp giải :

- Bài toán cho biết hiệu của hai số là $57$, bài toán yêu cầu tìm tổng của hai số đó. Muốn tìm tổng của hai số, ta phải tìm hai số đó trước.

- Theo đề bài giảm số lớn đi $4$ lần thì ta được số bé nên tỉ số của hai số là $\dfrac{1}{4}$. Ta biểu diễn số bé bằng 1 phần, số lớn bằng $4$ phần như thế. Ta tìm hai số theo công thức:

Số bé = Giá trị một phần × số phần của số bé

hoặc

Số lớn = Giá trị một phần × số phần của số lớn

Lời giải chi tiết :

Theo đề bài giảm số lớn đi $4$ lần thì ta được số bé nên tỉ số của hai số là $\dfrac{1}{4}$.

Ta có sơ đồ:

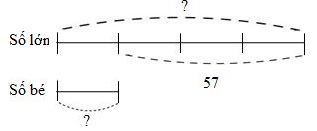
Theo sơ đồ, hiệu số phần bằng nhau là:

$4 - 1 = 3$ (phần)

Giá trị một phần hay số bé là:

$57:3 = 19$

Số lớn là:

$19 + 57 = 76$

Tổng hai số đó là:

$76 + 19 = 95$

Đáp số: $95$

Vậy số thích hợp điền vào ô trống là $95$.

Câu 7 :

A. $259kg$ gạo tẻ; $41kg$ gạo nếp

B. $229kg$ gạo tẻ; $71kg$ gạo nếp

C. $225kg$ gạo tẻ; $75kg$ gạo nếp

D. $400kg$ gạo tẻ; $100kg$ gạo nếp

Đáp án

B. $229kg$ gạo tẻ; $71kg$ gạo nếp

Phương pháp giải :

- Đề bài cho tổng số gạo ban đầu nhưng lại cho tỉ số giữa gạo nếp và gạo tẻ lúc sau. Để tính được lúc đầu người ta có bao nhiêu ki-lô-gam gạo mỗi loại, ta sẽ đi tìm xem sau khi bán thì mỗi loại còn lại bao nhiêu ki-lô-gam gạo.

- Ban đầu có $3$ tạ gạo, tức là có $300kg$ gạo, người đó bán đi $65kg$ gạo tẻ và $30kg$ gạo nếp nên số gạo còn lại lúc sau là $300 - 65 - 30 = 205kg$. Từ đây ta đưa được về bài toán dạng tìm hai số khi biết tổng và tỉ số của hai số.

Theo bài ra số gạo nếp còn lại bằng $\dfrac{1}{4}$ số gạo tẻ nên ta vẽ sơ đồ biểu thị số gạo nếp gồm $1$ phần, số gạo tẻ gồm $4$ phần như thế. Cọi số gạo nếp là số bé, số gạo tẻ là số lớn, ta tìm hai số theo công thức:

Số bé = Giá trị một phần × số phần của số bé

hoặc

Số lớn = Giá trị một phần × số phần của số lớn.

Lời giải chi tiết :

Đổi $3$ tạ $ = 300kg$.

Sau khi bán, người đó còn lại số ki-lô-gam gạo tẻ và gạo nếp là:

$300 - 65 - 30 = 205\,(kg)$

Ta có sơ đồ biểu diễn số gạo còn lại sau khi bán:

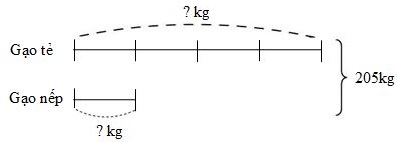
Theo sơ đồ, tổng số phần bằng nhau là:

$4 + 1 = 5$ (phần)

Giá trị một phần hay số gạo nếp còn lại sau khi bán là:

$205:5 = 41\,(kg)$

Ban đầu người đó có số ki-lô-gam gạo nếp là:

$41 + 30 = 71\,(kg)$

Ban đầu người đó có số ki-lô-gam gạo nếp là:

$300 - 71 = 229\,(kg)$

Đáp số: $229kg$ gạo tẻ; $71kg$ gạo nếp

Câu 8 :

Điền số thích hợp vào ô trống:

Đàn gà nhà An có một số con gà trống và gà mái, trong đó có $48$ con gà trống và số gà mái bằng $\dfrac{2}{5}$ số gà của cả đàn.

Vậy nhà An nuôi được

con gà mái.

Đáp án

Vậy nhà An nuôi được

con gà mái.

Phương pháp giải :

- Có $48$ con gà trống nên $48$ là hiệu số con gà của cả đàn và số con gà mái. Từ đây ta đưa được về bài toán dạng tìm hai số khi biết hiệu và tỉ số của hai số.

- Theo bài ra, số gà mái bằng $\dfrac{2}{5}$ số gà của cả đàn nên ta vẽ sơ đồ biểu diễn số gà mái là $2$ phần, số gà của cả đàn bằng $5$ phần như thế. Coi số gà mái là số bé, số gà cả đàn là số lớn, ta tìm hai số theo công thức:

Số bé = Giá trị một phần × số phần của số bé

hoặc

Số lớn = Giá trị một phần × số phần của số lớn.

Lời giải chi tiết :

Có $48$ con gà trống nên hiệu số con gà của cả đàn và số con gà mái là $48$ con.

Ta có sơ đồ:

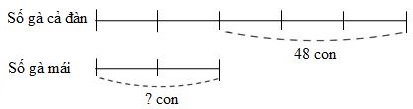
Theo sơ đồ, hiệu số phần bằng nhau là:

$5 - 2 = 3$ (phần)

Giá trị một phần là:

$48:3 = 16$ (con)

Nhà An nuôi số con gà mái là:

$16 \times 2 = 32$ (con)

Đáp số: $32$ con gà mái.

Vậy số thích hợp điền vào ô trống là $32$.

Câu 9 :

Điền số thích hợp vào ô trống:

Tổng của hai số là $374$. Nếu viết thêm chữ số $0$ vào bên phải số bé thì được số lớn.

Vậy số bé là

Số lớn là

Đáp án

Vậy số bé là

Số lớn là

Phương pháp giải :

Bài toán cho biết tổng của hai số là $374.$ Nếu viết thêm chữ số $0$ vào bên phải số bé thì được số lớn nên số lớn gấp $10$ lần số bé. Từ đây ta đưa được về bài toán dạng tìm hai số khi biết tổng và tỉ số của hai số.

Ta vẽ sơ đồ biểu thị số bé là $1$ phần, số lớn là $10$ phần như thế, ta tìm hai số theo công thức:

Số bé = Giá trị một phần × số phần của số bé

hoặc Số lớn = Giá trị một phần × số phần của số lớn.

Lời giải chi tiết :

Nếu viết thêm chữ số $0$ vào bên phải số bé thì được số lớn nên số lớn gấp $10$ lần số bé.

Ta có sơ đồ:

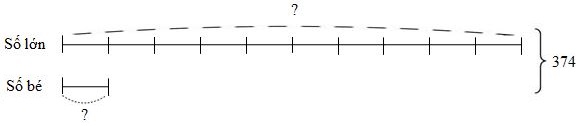
Theo sơ đồ, tổng số phần bằng nhau là:

$10 + 1 = 11$ (phần)

Giá trị một phần hay số bé là:

$374:11 = 34\,$

Số lớn là:

$34 \times 10 = 340\,$

Đáp số: số bé: $34$; số lớn: $340$.

Vậy hai số điền vào ô trống theo thứ tự là $34;\,340$.

Câu 10 :

Hai năm trước tuổi mẹ gấp $8$ lần tuổi con. Sau ba năm nữa tổng số tuổi của hai mẹ con là $46$ tuổi. Hỏi năm nay mẹ bao nhiêu tuổi, con bao nhiêu tuổi?

A. Con $4$ tuổi; mẹ $32$ tuổi

B. Con $6$ tuổi; mẹ $34$ tuổi

C. Con $7$ tuổi; mẹ $35$ tuổi

D. Con $9$ tuổi; mẹ $37$ tuổi

Đáp án

B. Con $6$ tuổi; mẹ $34$ tuổi

Phương pháp giải :

- Tìm số tuổi của hai mẹ con hiện nay, ta dựa vào tổng số tuổi của hai mẹ con sau ba năm nữa và tỉ số về số tuổi của hai mẹ con hai năm trước.

- Vì mỗi năm mỗi người tăng thêm 1 tuổi và tổng số tuổi của hai mẹ con sau ba năm nữa là $46$ tuổi nên tổng số tuổi của hai mẹ con hiện nay là $46 - 3 - 3 = 40$ tuổi. Từ đó ta tìm được tổng số tuổi của hai mẹ con hai năm trước là $40 - 2 - 2 = 36$ tuổi. Từ đây ta đưa được về bài toán dạng tìm hai số khi biết tổng và tỉ số của hai số.

- Ta vẽ sơ đồ biểu diễn tuổi con hai năm trước là $1$ phần, tuổi mẹ hai năm trước là $6$ phần. Coi số tuổi của con là số bé, số tuổi của mẹ là số lớn, ta tìm hai số theo công thức:

Số bé = giá trị một phần × số phần của số bé

hoặc Số lớn = giá trị một phần × số phần của số lớn.

Lời giải chi tiết :

Tổng số tuổi của hai mẹ con hiện nay là

$46 - 3 - 3 = 40$ (tuổi)

Tổng số tuổi của hai mẹ con hai năm trước là:

$40 - 2 - 2 = 36$ (tuổi)

Ta có sơ đồ tuổi của hai mẹ con hai năm trước:

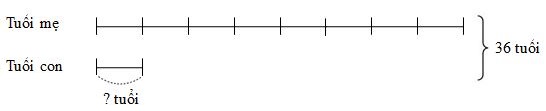
Theo sơ đồ, tổng số phần bằng nhau là:

$8 + 1 = 9$ (phần)

Giá trị một phần hay tuổi con hai năm trước là:

$36:9 = 4$ (tuổi)

Tuổi con hiện nay là:

$4 + 2 = 6\,$ (tuổi)

Tuổi mẹ hiện nay là:

$40 - 6 = 34\,$ (tuổi)

Đáp số: Con $6$ tuổi; mẹ $34$ tuổi

Trắc nghiệm: Ôn tập và bổ sung về giải toán Toán 5

Luyện tập và củng cố kiến thức Ôn tập và bổ sung về giải toán Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Ôn tập: Bảng đơn vị đo độ dài Toán 5

Luyện tập và củng cố kiến thức Ôn tập: Bảng đơn vị đo độ dài Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Ôn tập: Bảng đơn vị đo khối lượng Toán 5

Luyện tập và củng cố kiến thức Ôn tập: Bảng đơn vị đo khối lượng Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Đề-ca-mét vuông. Héc-tô-mét vuông. Héc-ta Toán 5

Luyện tập và củng cố kiến thức Đề-ca-mét vuông. Héc-tô-mét vuông. Héc-ta Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Mi-li-mét vuông. Bảng đơn vị đo diện tích Toán 5

Luyện tập và củng cố kiến thức Mi-li-mét vuông. Bảng đơn vị đo diện tích Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Ôn tập chương 1 Toán 5

Luyện tập và củng cố kiến thức Ôn tập chương 1 Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Luyện tập chung về phân số và hỗn số Toán 5

Luyện tập và củng cố kiến thức Luyện tập chung về phân số và hỗn số Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Hỗn số (tiếp theo) Toán 5

Luyện tập và củng cố kiến thức Hỗn số (tiếp theo) Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Hỗn số Toán 5

Luyện tập và củng cố kiến thức Hỗn số Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Ôn tập: Phép nhân và phép chia hai phân số Toán 5

Luyện tập và củng cố kiến thức Ôn tập: Phép nhân và phép chia hai phân số Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Ôn tập: Phép cộng và phép trừ hai phân số Toán 5

Luyện tập và củng cố kiến thức Ôn tập: Phép cộng và phép trừ hai phân số Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Phân số thập phân Toán 5

Luyện tập và củng cố kiến thức Phân số thập phân Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Ôn tập: So sánh hai phân số (tiếp) Toán 5

Luyện tập và củng cố kiến thức Ôn tập: So sánh hai phân số (tiếp) Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Ôn tập: So sánh hai phân số Toán 5

Luyện tập và củng cố kiến thức Ôn tập: So sánh hai phân số Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Ôn tập khái niệm về phân số. Tính chất cơ bản của phân số Toán 5

Luyện tập và củng cố kiến thức Ôn tập khái niệm về phân số. Tính chất cơ bản của phân số Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Bài giải mới nhất

Trắc nghiệm: Ôn tập về giải toán Toán 5

Báo lỗi góp ý