-
Chương 1. Ôn tâp và bổ sung về phân số. Giải toán liên quan đến tỉ lệ. Bảng đơn vị đo diện tích
- Ôn tập khái niệm về phân số. Tính chất cơ bản của phân số
- Ôn tập: So sánh hai phân số
- Ôn tập: So sánh hai phân số (tiếp)
- Phân số thập phân
- Ôn tập: Phép cộng và phép trừ hai phân số
- Ôn tập: Phép nhân và phép chia hai phân số
- Hỗn số
- Hỗn số (tiếp theo)
- Luyện tập chung về phân số và hỗn số
- Ôn tập về giải toán
- Ôn tập và bổ sung về giải toán
- Ôn tập: Bảng đơn vị đo độ dài
- Ôn tập: Bảng đơn vị đo khối lượng
- Đề-ca-mét vuông. Héc-tô-mét vuông. Héc-ta
- Mi-li-mét vuông. Bảng đơn vị đo diện tích
- Ôn tập chương 1
-
Chương 2. Số thập phân. Các phép tính với số thập phân
- Khái niệm số thập phân
- Hàng của số thập phân. Đọc, viết số thập phân
- Số thập phân bằng nhau. So sánh hai số thập phân
- Viết các số đo độ dài dưới dạng số thập phân
- Viết các số đo khối lượng dưới dạng số thập phân
- Viết các số đo diện tích dưới dạng số thập phân
- Luyện tập về số thập phân
- Phép cộng số thập phân. Tổng nhiều số thập phân
- Phép trừ hai số thập phân
- Luyện tập về phép cộng và phép trừ số thập phân
- Nhân một số thập phân với một số tự nhiên
- Nhân một số thập phân với 10, 100, 1000, …
- Nhân một số thập phân với một số thập phân
- Luyện tập về phép nhân số thập phân
- Chia một số thập phân cho một số tự nhiên
- Chia một số thập phân cho 10, 100, 1000, …
- Chia một số tự nhiên cho một số tự nhiên mà thương tìm được là một số thập phân
- Chia một số tự nhiên cho một số thập phân
- Chia một số thập phân cho một số thập phân
- Luyện tập về phép chia số thập phân
- Tỉ số phần trăm. Các phép tính với tỉ số phần trăm
- Giải toán về tỉ số phần trăm: Tìm tỉ số phần trăm của hai số
- Giải toán về tỉ số phần trăm: Tìm giá trị phần trăm của một số
- Giải toán về tỉ số phần trăm: Tìm một số khi biết giá trị phần trăm của số đó
- Giải toán về tỉ số phần trăm: Tỉ số phần trăm liên quan đến mua bán
- Ôn tập chương 2
-
Chương 3. Hình học
- Hình tam giác. Diện tích hình tam giác
- Hình thang. Diện tích hình thang
- Hình tròn. Đường tròn. Chu vi hình tròn
- Diện tích hình tròn
- Luyện tập về diện tích các hình
- Hình hộp chữ nhật. Hình lập phương
- Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật
- Diện tích xung quanh và diện tích toàn phần của hình lập phương
- Thể tích của một hình. Xăng-ti-mét khối. Đề-xi-mét khối. Mét khối
- Thể tích hình hộp chữ nhật
- Thể tích hình lập phương
- Ôn tập chương 3
-
Chương 4. Số đo thời gian. Toán chuyển động đều
- Bảng đơn vị đo thời gian
- Cộng số đo thời gian
- Trừ số đo thời gian
- Nhân số đo thời gian với một số
- Chia số đo thời gian cho một số
- Luyện tập về số đo thời gian và các phép tính với số đo thời gian
- Vận tốc
- Quãng đường
- Thời gian
- Hai vật chuyển động ngược chiều
- Hai vật chuyển động cùng chiều
- Chuyển động trên dòng nước
-
Chương 5. Ôn tập
- Ôn tập về số tự nhiên
- Ôn tập về phân số
- Ôn tập về số thập phân
- Ôn tập về đo độ dài và đo khối lượng
- Ôn tập về đo diện tích và đo thể tích
- Ôn tập về số đo thời gian
- Ôn tập về phép cộng
- Ôn tập về phép trừ
- Ôn tập về phép nhân
- Ôn tập về phép chia
- Ôn tập các phép tính với số đo thời gian
- Ôn tập về hình học: Tính chu vi, diện tích một số hình
- Ôn tập về hình học: Tính diện tích, thể tích một số hình
Trắc nghiệm: Ôn tập về phân số Toán 5
Đề bài
Cho hình vẽ sau:
Phân số chỉ phần đã tô màu là:
A. \(\dfrac{9}{{20}}\)
B. \(\dfrac{9}{{11}}\)
C. \(\dfrac{{11}}{{20}}\)
D. \(\dfrac{{11}}{9}\)
Cho hình vẽ sau:
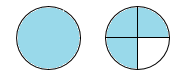
Hỗn số chỉ phần đã tô màu của hình vẽ trên là:
A. $\dfrac{7}{4}$
B. \(2\dfrac{3}{4}\)
C. \(2\dfrac{4}{3}\)
D. \(1\dfrac{3}{4}\)
Một đội công nhân phải mắc xong \(1km\) đường dây điện trong một ngày. Buổi sáng đội đã mắc được \(456m\) và buổi chiều đội đã hoàn thành công việc. Vậy phân số chỉ phần công việc làm được buổi chiều là:
A. \(\dfrac{{456}}{{1000}}\)
B. \(\dfrac{{544}}{{1000}}\)
C. \(\dfrac{{544}}{1}\)
D. \(\dfrac{{456}}{{100}}\)
Trong các phân số sau, phân số nào là phân số tối giản?
A. \(\dfrac{6}{9}\)
B. \(\dfrac{{15}}{{20}}\)
C. \(\dfrac{{13}}{{26}}\)
D. \(\dfrac{{15}}{{22}}\)
Rút gọn phân số \(\dfrac{{75}}{{45}}\) ta được phân số tối giản là:
A. \(\dfrac{{15}}{9}\)
B. \(\dfrac{5}{3}\)
C. \(\dfrac{7}{5}\)
D. \(\dfrac{{25}}{{15}}\)
Trong các phân số sau, phân số nào bằng với phân số \(\dfrac{8}{{12}}\)?
A. \(\dfrac{2}{3}\)
B. \(\dfrac{{16}}{{24}}\)
C. \(\dfrac{{48}}{{72}}\)
D. Cả A, B, C đều đúng
Quy đồng mẫu số hai phân số \(\dfrac{2}{3}\,;\,\,\dfrac{3}{4}\) ta đươc hai phân số lần lượt là:
A. \(\dfrac{{15}}{{24}};\,\,\dfrac{{21}}{{24}}\)
B. \(\dfrac{6}{9};\,\,\dfrac{6}{8}\)
C. \(\dfrac{8}{{12}};\,\,\dfrac{9}{{12}}\)
D. \(\dfrac{9}{{12}};\,\,\dfrac{8}{{12}}\)
Quy đồng mẫu số hai phân số \(\dfrac{5}{9}\,;\,\,\dfrac{{31}}{{36}}\) sao cho mẫu số chung nhỏ nhất ta đươc hai phân số lần lượt là:
Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{2}{9} \cdot \cdot \cdot \dfrac{2}{{15}}\)
A. \( > \)
B. \( < \)
C. \( = \)
\(\dfrac{5}{7} \cdot \cdot \cdot \dfrac{4}{5}\)
Dấu thích hợp điền vào chỗ chấm là:
A. \(<\)
B. \(>\)
C. \(=\)
Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{{216}}{{217}} \cdot \cdot \cdot \dfrac{{2016}}{{2017}}\)
A. \( > \)
B. \( < \)
C. \( = \)
Sắp xếp các phân số sau theo thứ tự từ bé đến lớn:
\(\dfrac{4}{9}\)
\(\dfrac{2}{3}\)
\(\dfrac{9}{7}\)
\(\dfrac{1}{6}\)
Lời giải và đáp án
Cho hình vẽ sau:
Phân số chỉ phần đã tô màu là:
A. \(\dfrac{9}{{20}}\)
B. \(\dfrac{9}{{11}}\)
C. \(\dfrac{{11}}{{20}}\)
D. \(\dfrac{{11}}{9}\)
C. \(\dfrac{{11}}{{20}}\)
Quan sát hình vẽ, tìm ô vuông được tô màu và tổng số ô vuông, từ đó tìm được phân số.
Quan sát hình vẽ ta thấy có tất cả \(20\) ô vuông, trong đó có \(11\) ô vuông được tô màu. Vậy phân số chỉ số ô vuông đã tô màu trong hình là \(\dfrac{{11}}{{20}}\).
Cho hình vẽ sau:
Hỗn số chỉ phần đã tô màu của hình vẽ trên là:
A. $\dfrac{7}{4}$
B. \(2\dfrac{3}{4}\)
C. \(2\dfrac{4}{3}\)
D. \(1\dfrac{3}{4}\)
D. \(1\dfrac{3}{4}\)
Quan sát hình vẽ, tìm số hình tròn được tô màu và số phần nhỏ của hình tròn được tô màu, từ đó tìm được hỗn số.
Quan sát hình vẽ ta thấy có tất cả \(1\) hình tròn được tô màu toàn bộ, \(1\) hình tròn chia làm \(4\) phần và được tô màu \(3\) phần.
Vậy hỗn số chỉ phần đã tô màu trong hình là \(1\dfrac{3}{4}\).
Một đội công nhân phải mắc xong \(1km\) đường dây điện trong một ngày. Buổi sáng đội đã mắc được \(456m\) và buổi chiều đội đã hoàn thành công việc. Vậy phân số chỉ phần công việc làm được buổi chiều là:
A. \(\dfrac{{456}}{{1000}}\)
B. \(\dfrac{{544}}{{1000}}\)
C. \(\dfrac{{544}}{1}\)
D. \(\dfrac{{456}}{{100}}\)
B. \(\dfrac{{544}}{{1000}}\)
- Đổi \(1km = 1000m\).
- Tìm số mét đường dây điện đội công nhân mắc được trong buổi chiều \( = \,1000m - 456m\).
- Viết phân số chỉ phần công việc làm được buổi chiều: tử số là số mét đường dây điện đội công nhân mắc được trong buổi chiều, mẫu số là số mét đường dây điện đội công nhân phải mắc được trong cả ngày.
Đổi \(1km = 1000m\)
Đội công nhân mắc được trong buổi chiều số mét đường dây điện là:
\(1000 - 456 = 544(m)\)
Vậy phân số chỉ phần công việc làm được buổi chiều là \(\dfrac{{544}}{{1000}}\).
Trong các phân số sau, phân số nào là phân số tối giản?
A. \(\dfrac{6}{9}\)
B. \(\dfrac{{15}}{{20}}\)
C. \(\dfrac{{13}}{{26}}\)
D. \(\dfrac{{15}}{{22}}\)
D. \(\dfrac{{15}}{{22}}\)
- Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho số nào lớn hơn \(1\).
- Rút gọn các phân số đã cho rồi tìm phân số tối giản.
Ta có:
$\dfrac{6}{9} = \dfrac{{6:3}}{{9:3}} = \dfrac{2}{3}$;
$\dfrac{{15}}{{20}} = \dfrac{{15:5}}{{20:5}} = \dfrac{3}{4}$ ;
$\dfrac{{13}}{{26}} = \dfrac{{13:13}}{{26:13}} = \dfrac{1}{2}$ ;
Phân số \(\dfrac{{15}}{{22}}\) có tử số tử số và mẫu số không cùng chia hết cho số nào lớn hơn \(1\).
Vậy trong các phân số đã cho, phân số tối giản là \(\dfrac{{15}}{{22}}\).
Rút gọn phân số \(\dfrac{{75}}{{45}}\) ta được phân số tối giản là:
A. \(\dfrac{{15}}{9}\)
B. \(\dfrac{5}{3}\)
C. \(\dfrac{7}{5}\)
D. \(\dfrac{{25}}{{15}}\)
B. \(\dfrac{5}{3}\)
- Xét xem cả tử số và mẫu số của phân số đó cùng chia hết cho số tự nhiên nào (khác \(1\)) không?
- Chia cả tử số và mẫu số của phân số đó cho số tự nhiên vừa tìm được.
- Cứ làm như thế cho đến khi tìm được phân số tối giản.
Ta có:
\(\dfrac{{75}}{{45}} = \dfrac{{75:3}}{{45:3}} = \dfrac{{25}}{{15}} = \dfrac{{25:5}}{{15:5}} = \dfrac{5}{3}\)
hoặc \(\dfrac{{75}}{{45}} = \dfrac{{75:5}}{{45:5}} = \dfrac{{15}}{9} = \dfrac{{15:3}}{{9:3}} = \dfrac{5}{3}\); …
Trong các phân số sau, phân số nào bằng với phân số \(\dfrac{8}{{12}}\)?
A. \(\dfrac{2}{3}\)
B. \(\dfrac{{16}}{{24}}\)
C. \(\dfrac{{48}}{{72}}\)
D. Cả A, B, C đều đúng
D. Cả A, B, C đều đúng
Sử dụng tính chất cơ bản của phân số:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác \(0\) thì được một phân số bằng phân số đã cho.
- Nếu chia cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác \(0\) thì được một phân số bằng phân số đã cho.
Ta có:
$\dfrac{8}{{12}} = \dfrac{{8:4}}{{12:4}} = \dfrac{2}{3}$ ;
$\dfrac{8}{{12}} = \dfrac{{8 \times 2}}{{12 \times 2}} = \dfrac{{16}}{{24}}$ ;
$\dfrac{8}{{12}} = \dfrac{{8 \times 6}}{{12 \times 6}} = \dfrac{{48}}{{72}}$.
Vậy cả A, B, C đều đúng.
Quy đồng mẫu số hai phân số \(\dfrac{2}{3}\,;\,\,\dfrac{3}{4}\) ta đươc hai phân số lần lượt là:
A. \(\dfrac{{15}}{{24}};\,\,\dfrac{{21}}{{24}}\)
B. \(\dfrac{6}{9};\,\,\dfrac{6}{8}\)
C. \(\dfrac{8}{{12}};\,\,\dfrac{9}{{12}}\)
D. \(\dfrac{9}{{12}};\,\,\dfrac{8}{{12}}\)
C. \(\dfrac{8}{{12}};\,\,\dfrac{9}{{12}}\)
- Tìm mẫu số chung của hai phân số, ở bài này ta chọn \(MSC = 3 \times 4 = 12\).
- Lấy cả tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
- Lấy cả tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.
Ta có: \(MSC = 12\). Quy đồng mẫu số hai phân số ta có:
$\dfrac{2}{3} = \dfrac{{2 \times 4}}{{3 \times 4}} = \dfrac{8}{{12}}$
$\dfrac{3}{4} = \dfrac{{3 \times 3}}{{4 \times 3}} = \dfrac{9}{{12}}$.
Vậy quy đồng mẫu số hai phân số \(\dfrac{2}{3};\,\,\dfrac{3}{4}\) ta đươc hai phân số lần lượt là \(\dfrac{8}{{12}};\,\,\dfrac{9}{{12}}\).
Chọn C.
Quy đồng mẫu số hai phân số \(\dfrac{5}{9}\,;\,\,\dfrac{{31}}{{36}}\) sao cho mẫu số chung nhỏ nhất ta đươc hai phân số lần lượt là:
- Tìm mẫu số chung nhỏ nhất: ta thấy \(36\) chia hết cho \(9\) nên mẫu số chung nhỏ nhất là \(36\).
- Quy đồng phân số \(\dfrac{5}{9}\) bằng cách nhân cả tử số và mẫu số với \(4\) (do \(36:9 = 4\))
- Giữ nguyên phân số \(\dfrac{{31}}{{36}}\).
Ta thấy \(36\) chia hết cho \(9\) nên mẫu số chung nhỏ nhất là \(36\).
Quy đồng mẫu số hai phân số \(\dfrac{5}{9};\,\,\dfrac{{31}}{{36}}\) ta có:
\(\dfrac{5}{9} = \dfrac{{5 \times 4}}{{9 \times 4}} = \dfrac{{20}}{{36}};\,\)
Giữ nguyên phân số\(\dfrac{{31}}{{36}}\).
Vậy ta điền phân số thứ nhất là \(\dfrac{{20}}{{36}}\) , phân số thứ hai là \(\dfrac{{31}}{{36}}\).
Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{2}{9} \cdot \cdot \cdot \dfrac{2}{{15}}\)
A. \( > \)
B. \( < \)
C. \( = \)
A. \( > \)
Dựa vào quy tắc so sánh hai phân số có cùng tử số:
Quy tắc: Trong hai phân số có cùng tử số:
+) Phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.
+) Phân số nào có mẫu số lớn hơn thì phân số đó bé hơn.
+) Nếu mẫu số bằng nhau thì hai phân số đó bằng nhau.
Ta thấy hai phân số \(\dfrac{2}{9}\) và \(\dfrac{2}{{15}}\) đều có tử số là \(2\) và \(9 < 15\) nên \(\dfrac{2}{9} > \dfrac{2}{{15}}\).
Vậy \(\dfrac{2}{9} > \dfrac{2}{{15}}\).
\(\dfrac{5}{7} \cdot \cdot \cdot \dfrac{4}{5}\)
Dấu thích hợp điền vào chỗ chấm là:
A. \(<\)
B. \(>\)
C. \(=\)
A. \(<\)
Quy đồng mẫu số hai phân số rồi so sánh hai phân số sau khi đã quy đồng theo quy tắc:
Trong hai phân số có cùng mẫu số:
+) Phân số nào có tử số bé hơn thì phân số đó bé hơn.
+) Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
+) Nếu tử số bằng nhau thì hai phân số đó bằng nhau.
Ta có: \(MSC = 35\). Quy đồng mẫu số hai phân số ta có:
\(\dfrac{5}{7} = \dfrac{{5 \times 5}}{{7 \times 5}} = \dfrac{{25}}{{35}};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{4}{5} = \dfrac{{4 \times 7}}{{5 \times 7}} = \dfrac{{28}}{{35}}\)
Mà \(\dfrac{{25}}{{35}} < \dfrac{{28}}{{35}}\).
Do đó \(\dfrac{5}{7} < \dfrac{4}{5}\).
Vậy dấu thích hợp điền vào chỗ chấm là \( < \).
Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{{216}}{{217}} \cdot \cdot \cdot \dfrac{{2016}}{{2017}}\)
A. \( > \)
B. \( < \)
C. \( = \)
B. \( < \)
Sử dụng phương pháp so sánh bằng phần bù
- Phần bù với \(1\) của phân số là hiệu giữa \(1\) và phân số đó.
- Quy tắc: Trong hai phân số, phân số nào có phần bù lớn hơn thì phân số đó nhỏ hơn và ngược lại.
Phần bù của \(\dfrac{{216}}{{217}}\) là \(1 - \dfrac{{216}}{{217}} = \dfrac{{217}}{{217}} - \dfrac{{216}}{{217}} = \dfrac{1}{{217}}\)
Phần bù của \(\dfrac{{2016}}{{2017}}\) là \(1 - \dfrac{{2016}}{{2017}} = \dfrac{{2017}}{{2017}} - \dfrac{{2016}}{{2017}} = \dfrac{1}{{2017}}\)
Ta có: \(\dfrac{1}{{217}} > \dfrac{1}{{2017}}\).
Do đó \(\dfrac{{216}}{{217}} < \dfrac{{2016}}{{2017}}\).
Sắp xếp các phân số sau theo thứ tự từ bé đến lớn:
\(\dfrac{4}{9}\)
\(\dfrac{2}{3}\)
\(\dfrac{9}{7}\)
\(\dfrac{1}{6}\)
\(\dfrac{1}{6}\)
\(\dfrac{4}{9}\)
\(\dfrac{2}{3}\)
\(\dfrac{9}{7}\)
- Phân số \(\dfrac{9}{7}\) có tử số lớn hơn mẫu số nên \(\dfrac{9}{7} > 1\) và các phân số \(\dfrac{4}{9};\,\dfrac{2}{3};\,\dfrac{1}{6}\) đều có tử số nhỏ hơn mẫu số nên các phân số này đều nhỏ hơn \(1\).
- Quy đồng mẫu số các phân số \(\dfrac{4}{9};\,\dfrac{2}{3};\,\dfrac{1}{6}\) rồi so sánh ba phân số sau khi đã quy đồng.
Ta có : \(\dfrac{9}{7} > 1; \quad \,\dfrac{4}{9} < 1; \quad \,\dfrac{2}{3} < 1; \quad \dfrac{1}{6} < 1\).
Ta sẽ quy đồng mẫu số các phân số \(\dfrac{4}{9};\,\dfrac{2}{3};\,\dfrac{1}{6}\) rồi so sánh ba phân số sau khi đã quy đồng.
\(MSC = 18\). Quy đồng mẫu số ba phân số ta có:
\(\dfrac{4}{9} = \dfrac{{4 \times 2}}{{9 \times 2}} = \dfrac{8}{{18}};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{2}{3} = \dfrac{{2 \times 6}}{{3 \times 6}} = \dfrac{{12}}{{18}}\)
\(\dfrac{1}{6} = \dfrac{{1 \times 3}}{{6 \times 3}} = \dfrac{3}{{18}}\).
Mà \(\dfrac{3}{{18}} < \dfrac{8}{{18}} < \dfrac{{12}}{{18}}\) nên \(\dfrac{1}{6} < \dfrac{4}{9} < \dfrac{2}{3}\).
Vậy \(\dfrac{1}{6} < \dfrac{4}{9} < \dfrac{2}{3} < \dfrac{9}{7}\).
Dãy các phân số được sắp xếp theo thứ tự từ bé đến lớn là \(\dfrac{1}{6}\;;\,\,\,\dfrac{4}{9}\;;\,\,\,\dfrac{2}{3}\;;\,\,\,\dfrac{9}{7}\).
Luyện tập và củng cố kiến thức Ôn tập về số thập phân Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về đo độ dài và đo khối lượng Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về đo diện tích và đo thể tích Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về số đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về phép cộng Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về phép trừ Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về phép nhân Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về phép chia Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập các phép tính với số đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về hình học: Tính chu vi, diện tích một số hình Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về hình học: Tính diện tích, thể tích một số hình Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về số tự nhiên Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
