Bài tập trắc nghiệm Toán 5 có đáp án Bài tập trắc nghiệm Chương 4 Số đo thời gian, toán chuy..

Trắc nghiệm: Chuyển động trên dòng nước Toán 5

Đề bài

Xem đáp án

Làm bài tập

Đề bài

Câu 1 :

Vận tốc xuôi dòng của ca nô bằng vận tốc thực của ca nô trừ đi vận tốc dòng nước. Phát biểu đó đúng hay sai?

A. Đúng

B. Sai

Câu 2 :

Trong các công thức sau, công thức nào đúng?

A. Vận tốc xuôi dòng $ = $ vận tốc thực của vật $ + $ vận tốc dòng nước.

B. Vận tốc ngược dòng $ = $ vận tốc thực của vật $ - $ vận tốc dòng nước.

C. Vận tốc thực của vật $ = $ (vận tốc xuôi dòng $ + $ vận tốc ngược dòng) $:\,2$

D. Cả A, B, C đều đúng

Câu 3 :

Vận tốc ca nô khi nước lặng là $15$ km/giờ. Vận tốc dòng nước là $2$ km/giờ. Vận tốc của ca nô khi đi xuôi dòng là:

A. $19$ km/giờ

B. $8,5$ km/giờ

C. $13$ km/giờ

D. $17$ km/giờ

Câu 4 :

Điền số thích hợp vào ô trống:

Vận tốc ca nô khi nước lặng là $24$ km/giờ. Vận tốc dòng nước bằng $\dfrac{1}{8}$ vận tốc ca nô khi nước lặng.

Vận tốc của ca nô khi đi ngược dòng là

km/giờ.

Câu 5 :

Điền số thích hợp vào ô trống:

Một thuyền máy khi đi xuôi dòng có vận tốc là $28$ km/giờ, khi đi ngược dòng có vận tốc là $24$ km/giờ.

Vây vận tốc của thuyển máy khi nước yên lặng là

km/giờ ;

vận tốc của dòng nước là

km/giờ.

Câu 6 :

Vận tốc của thuyền khi nước lặng là $18$ km/giờ. Vận tốc dòng nước là $2$ km/giờ. Quãng đường sông từ A đến B dài $15km$. Hỏi thuyền đi xuôi dòng từ A đến B hết bao nhiêu thời gian?

A. $40$ phút

B. $45$ phút

C. $50$ phút

D. $56,25$ phút

Câu 7 :

Điền số thích hợp vào ô trống:

Lúc $7$ giờ $40$ phút ca nô đi ngược dòng từ bến B và về bến A lúc $8$ giờ $20$ phút. Biết vận tốc của ca nô khi nước lặng là $27$ km/giờ và vận tốc dòng nước là $3$ km/giờ.

Vậy khoảng cách giữa hai bến A và bến B là

$km$.

Câu 8 :

Một chiếc thuyền đi xuôi dòng từ A đến B với vận tốc $27$ km/giờ. Tính vận tốc của thuyền khi đi ngược dòng, biết vận tốc của thuyền khi nước lặng gấp $8$ lần vận tốc dòng nước.

A. $15$ km/giờ

B. $18$ km/giờ

C. $21$ km/giờ

D. $24$ km/giờ

Câu 9 :

Hai bến sông A và B cách nhau $40km$. Lúc $7$ giờ $20$ phút, một ca nô đi xuôi dòng từ A đến B. Biết vận tốc của ca nô khi đi ngược dòng là $28$ km/giờ và vận tốc dòng nước là $2$ km/giờ. Hỏi ca nô đến B lúc mấy giờ?

A. $8$ giờ $15$ phút

B. $8$ giờ $35$ phút

C. $8$ giờ $40$ phút

D. $8$ giờ $50$ phút

Câu 10 :

Một ca nô đi xuôi dòng một khúc sông từ bến A đến bến B hết $2$ giờ $45$ phút. Biết vận tốc thực của ca nô là $27,5$ km/giờ, vận tốc dòng nước là $2,5$ km/giờ. Hỏi ca nô đi ngược dòng khúc sông từ bến B đến bến A hết bao nhiêu thời gian?

A. $3$ giờ

B. $3$ giờ $20$ phút

C. $3$ giờ $45$ phút

D. $3$ giờ $18$ phút

Câu 11 :

Hai bến sông A và B cách nhau $32km$. Cùng một lúc ca nô thứ nhất đi xuôi dòng từ A đến B và ca nô thứ hai đi ngược dòng từ B đến A. Hỏi sau bao lâu hai ca nô sẽ gặp nhau, biết vận tốc của hai ca nô khi nước lặng đều bằng $20$ km/giờ và vận tốc dòng nước là $2$ km/giờ.

A. $\,48$ phút

B. $\,45$ phút

C. $\,40$ phút

D. $\,36$ phút

Câu 12 :

Điền số thích hợp vào ô trống:

Một chiếc ca nô đi xuôi dòng từ A đến B mất $8$ giờ, đi ngược dòng từ B về A mất $10$ giờ. Mỗi giờ ca nô đi ngược dòng chậm hơn đi xuôi dòng là $5km$.

Vậy độ dài quãng sông AB là

$km$.

Lời giải và đáp án

Câu 1 :

Vận tốc xuôi dòng của ca nô bằng vận tốc thực của ca nô trừ đi vận tốc dòng nước. Phát biểu đó đúng hay sai?

A. Đúng

B. Sai

Đáp án

A. Đúng

B. Sai

Lời giải chi tiết :

Vận tốc xuôi dòng của ca nô bằng vận tốc thực của ca nô cộng với vận tốc dòng nước.

Vậy phát biểu đã cho là sai.

Câu 2 :

Trong các công thức sau, công thức nào đúng?

A. Vận tốc xuôi dòng $ = $ vận tốc thực của vật $ + $ vận tốc dòng nước.

B. Vận tốc ngược dòng $ = $ vận tốc thực của vật $ - $ vận tốc dòng nước.

C. Vận tốc thực của vật $ = $ (vận tốc xuôi dòng $ + $ vận tốc ngược dòng) $:\,2$

D. Cả A, B, C đều đúng

Đáp án

D. Cả A, B, C đều đúng

Lời giải chi tiết :

Ta có:

- Vận tốc xuôi dòng $ = $ vận tốc thực của vật $ + $ vận tốc dòng nước.

- Vận tốc ngược dòng $ = $ vận tốc thực của vật $ - $ vận tốc dòng nước.

- Vận tốc thực của vật $ = $ (vận tốc xuôi dòng $ + $ vận tốc ngược dòng) $:\,2$.

Vậy cả A, B, C đều đúng.

Câu 3 :

Vận tốc ca nô khi nước lặng là $15$ km/giờ. Vận tốc dòng nước là $2$ km/giờ. Vận tốc của ca nô khi đi xuôi dòng là:

A. $19$ km/giờ

B. $8,5$ km/giờ

C. $13$ km/giờ

D. $17$ km/giờ

Đáp án

D. $17$ km/giờ

Phương pháp giải :

Vận tốc xuôi dòng $ = $ vận tốc thực của vật $ + $ vận tốc dòng nước, hay

Vận tốc xuôi dòng $ = $ vận tốc của vật khi nước yên lặng $ + $ vận tốc dòng nước.

Lời giải chi tiết :

Vận tốc của ca nô khi đi xuôi dòng là:

$15 + 2 = 17$ (km/giờ)

Đáp số: $17$ km/giờ.

Câu 4 :

Điền số thích hợp vào ô trống:

Vận tốc ca nô khi nước lặng là $24$ km/giờ. Vận tốc dòng nước bằng $\dfrac{1}{8}$ vận tốc ca nô khi nước lặng.

Vận tốc của ca nô khi đi ngược dòng là

km/giờ.

Đáp án

Vận tốc ca nô khi nước lặng là $24$ km/giờ. Vận tốc dòng nước bằng $\dfrac{1}{8}$ vận tốc ca nô khi nước lặng.

Vận tốc của ca nô khi đi ngược dòng là

km/giờ.

Phương pháp giải :

- Tính vận tốc dòng nước ta lấy vận tốc của ca nô khi nước lặng nhân với $\dfrac{1}{8}$ hoặc lấy vận tốc của ca nô khi nước lặng chia cho $8$ rồi nhân với $1$.

- Vận tốc ngược dòng $ = $ vận tốc của vật khi nước yên lặng $ - $ vận tốc dòng nước.

Lời giải chi tiết :

Vận tốc dòng nước là:

$24 \times \dfrac{1}{8} = 3$ (km/giờ)

Vận tốc của ca nô khi đi ngược dòng là:

$24 - 3 = 21$ (km/giờ)

Đáp số: $21$ km/giờ.

Vậy đáp án đúng điền vào ô trống là $21$.

Câu 5 :

Điền số thích hợp vào ô trống:

Một thuyền máy khi đi xuôi dòng có vận tốc là $28$ km/giờ, khi đi ngược dòng có vận tốc là $24$ km/giờ.

Vây vận tốc của thuyển máy khi nước yên lặng là

km/giờ ;

vận tốc của dòng nước là

km/giờ.

Đáp án

Một thuyền máy khi đi xuôi dòng có vận tốc là $28$ km/giờ, khi đi ngược dòng có vận tốc là $24$ km/giờ.

Vây vận tốc của thuyển máy khi nước yên lặng là

km/giờ ;

vận tốc của dòng nước là

km/giờ.

Phương pháp giải :

Áp dụng các công thức:

- Vận tốc khi nước yên lặng $ = $ (vận tốc xuôi dòng $ + $ vận tốc ngược dòng) $:\,2$

- Vận tốc dòng nước $ = $ vận tốc xuôi dòng $ - $ vận tốc khi nước yên lặng.

Lời giải chi tiết :

Vận tốc của thuyền máy khi nước lặng là:

$(28 + 24):2 = 26$ (km/giờ)

Vận tốc dòng nước là:

$28 - 26 = 2$ (km/giờ)

Đáp số: Vận tốc của thuyền: $26$ km/giờ;

Vận tốc dòng nước: $2$ km/giờ.

Vậy đáp án điền vào ô trống theo thứ tự từ trên xuống dưới, từ trái sang phải là $26;\,\,\,2$.

Câu 6 :

A. $40$ phút

B. $45$ phút

C. $50$ phút

D. $56,25$ phút

Đáp án

B. $45$ phút

Phương pháp giải :

- Tìm vận tốc xuôi dòng $ = $ vận tốc thực của vật $ + $ vận tốc dòng nước.

- Tìm thời gian xuôi dòng $ = $ quãng đường $:$ vận tốc xuôi dòng;

Lời giải chi tiết :

Vận tốc của thuyền khi đi xuôi dòng là:

$18 + 2 = 20$ (km/giờ)

Thuyền đi xuôi dòng từ A đến B hết số thời gian là:

$15:20 = 0,75$ (giờ)

Đổi $0,75$ giờ $ = \,\,45$ phút

Đáp số: $45$ phút

Câu 7 :

Điền số thích hợp vào ô trống:

Vậy khoảng cách giữa hai bến A và bến B là

$km$.

Đáp án

Vậy khoảng cách giữa hai bến A và bến B là

$km$.

Phương pháp giải :

- Vận tốc ngược dòng $ = $ vận tốc khi nước yên lặng $ - $ vận tốc dòng nước.

- Tính thời gian đi ngược dòng từ bến B về bến A ta lấy thời gian lúc về đến bến A trừ đi thời gian lúc đi từ bến B.

- Quãng đường $ = $ vận tốc ngược dòng $ \times $ thời gian đi ngược dòng.

Lời giải chi tiết :

Vận tốc của ca nô khi đi ngược dòng là:

$27 - 3 = 24$ (km/giờ)

Ca nô đi từ bến B về bến A hết số thời gian là:

$8$ giờ $20$ phút $ - \,7$ giờ $40$ phút $ = \,40$ phút

Đổi $40$ phút $ = \dfrac{2}{3}$ giờ

Khoảng cách giữa hai bến A và bến B là:

$24 \times \dfrac{2}{3} = 16 \;(km)$

Đáp số: $16 km$.

Vậy đáp án đúng điền vào ô trống là $16$.

Câu 8 :

A. $15$ km/giờ

B. $18$ km/giờ

C. $21$ km/giờ

D. $24$ km/giờ

Đáp án

C. $21$ km/giờ

Phương pháp giải :

+) Vận tốc xuôi dòng $ = $ vận tốc thực của vật $ + $ vận tốc dòng nước.

Vậy tổng của vận tốc của thuyền khi nước lặng và vận tốc dòng nước là $27$km/giờ. Từ đó ta có tổng và tỉ số của vận tốc của thuyền khi nước lặng và vận tốc dòng nước. Đây là dạng toán tìm hai số khi biết tổng và tỉ số của hai số đó. Theo bài ra, vận tốc của thuyền khi nước lặng gấp $8$ lần vận tốc dòng nước nên ta vẽ sơ đồ biểu thị vận tốc dòng nước gồm $1$ phần bằng nhau, vận tốc của thuyền khi nước gồm $8$ phần như thế. Ta tìm hai số theo công thức sau:

Số bé $ = $ (tổng $:$ tổng số phần bằng nhau) $ \times $ số phần của số bé
Số lớn $ = $ (tổng $:$ tổng số phần bằng nhau) $ \times $ số phần của số lớn.

+) Vận tốc khi ngược dòng $=$ vận tốc khi nước yên lặng $–$ vận tốc dòng nước.

Lời giải chi tiết :

Ta có: vận tốc xuôi dòng $ = $ vận tốc thực của vật $ + $ vận tốc dòng nước.

Vậy tổng của vận tốc của thuyền khi nước lặng và vận tốc dòng nước là $27$ km/giờ.

Ta có sơ đồ:

Theo sơ đồ, tổng số phần bằng nhau là:

$8 + 1 = 9$ (phần)
Vận tốc dòng nước là:
            $27:9 \times 1 = 3$ (km/giờ)
Vận tốc của thuyền khi nước yên lặng là:
            $27 - 3 = 24$ (km/giờ)
Vận tốc của thuyền khi đi ngược dòng là:
            $24 - 3 = 21$ (km/giờ)
                                    Đáp số: $21$ km/giờ.

Câu 9 :

A. $8$ giờ $15$ phút

B. $8$ giờ $35$ phút

C. $8$ giờ $40$ phút

D. $8$ giờ $50$ phút

Đáp án

B. $8$ giờ $35$ phút

Phương pháp giải :

- Tính vận tốc của ca nô khi nước yên lặng và vận tốc xuôi dòng theo công thức:

Vận tốc khi nước lặng $=$ vận tốc ngược dòng $+$ vận tốc dòng nước;

Vận tốc xuôi dòng $=$ vận tốc khi nước lặng $+$ vận tốc dòng nước

- Tính thời gian đi xuôi dòng ta lấy độ dài từ bến A đến bến B chia cho vận tốc đi xuôi dòng.

- Tính thời gian ca nô đến B theo công thức:

Thời gian đến $=$ thời gian xuất phát $+$ thời gian đi $+$ thời gian nghỉ (nếu có).

Lời giải chi tiết :

Vận tốc của ca nô khi nước lặng là:

$28 + 2 = 30$ (km/giờ)

Vận tốc của ca nô khi đi xuôi dòng là:

$30 + 2 = 32$ (km/giờ)

Ca nô đi xuôi dòng từ A đến B hết số thời gian là:

$40:32 = 1,25$ (giờ)

Đổi $1,25$ giờ $ = \,1$ giờ $15$ phút

Ca nô đến B lúc:

$7$ giờ $20$ phút $ + \,1$ giờ $15$ phút $ = \,8$ giờ $35$ phút

Đáp số: $8$ giờ $35$ phút.

Câu 10 :

A. $3$ giờ

B. $3$ giờ $20$ phút

C. $3$ giờ $45$ phút

D. $3$ giờ $18$ phút

Đáp án

D. $3$ giờ $18$ phút

Phương pháp giải :

- Đổi $2$ giờ $45$ phút $ = 2,75$ giờ.

- Tính vận tốc xuôi dòng và vận tốc ngược dòng theo công thức:

Vận tốc xuôi dòng $ = $ vận tốc thực $ + $ vận tốc dòng nước;

Vận tốc ngược dòng $ = $ vận tốc thực $ - $ vận tốc dòng nước

- Tính độ dài từ bến A đến bến B ta lấy vận tốc đi xuôi dòng nhân với thời gian đi xuôi dòng.

- Tính thời gian đi ngược dòng ta lấy độ dài từ bến A đến bến B chia cho vận tốc đi ngược dòng.

Lời giải chi tiết :

Đổi $2$ giờ $45$ phút $ = 2,75$ giờ

Vận tốc của ca nô khi đi xuôi dòng là:

$27,5 + 2,5 = 30$ (km/giờ)

Vận tốc của ca nô khi đi ngược dòng là:

$27,5 - 2,5 = 25$ (km/giờ)

Độ dài từ bến A đến bến B là:

$30 \times 2,75 = 82,5\,\,(km)$

Ca nô đi ngược dòng khúc sông từ bến B đến bến A hết số thời gian là:

$82,5:25 = 3,3$ (giờ)

Đổi $3,3$ giờ $ = \,3$ giờ $18$ phút

Đáp số: $3$ giờ $18$ phút.

Câu 11 :

A. $\,48$ phút

B. $\,45$ phút

C. $\,40$ phút

D. $\,36$ phút

Đáp án

A. $\,48$ phút

Phương pháp giải :

- Tìm vận tốc ca nô thứ nhất đi từ A đến B:

Vận tốc ca nô đi từ A $=$ vận tốc xuôi dòng $ = $ vận tốc thực $ + $ vận tốc dòng nước.
- Tìm vận tốc ca nô thứ hai đi từ B đến A:

Vận tốc ca nô đi từ B $ = $ vận tốc ngược dòng $ = $ vận tốc thực $ - $ vận tốc dòng nước

- Từ đây ta có bài toán chuyển động của hai vật đi ngược chiều nhau. Tìm thời gian hai ca nô đi để gặp nhau theo công thức:

Thời gian găp nhau $ = $ quãng đường : tổng hai vận tốc.

Lời giải chi tiết :

Vận tốc của ca nô thứ nhất là:

$20 + 2 = 22$ (km/giờ)

Vận tốc của ca nô thứ hai là:

$20 - 2 = 18$ (km/giờ)

Hai ca nô gặp nhau sau khi đi số thời gian là:

$32:(22 + 18) = 0,8$ (giờ)

$0,8$ giờ $ = \,48$ phút

Đáp số: $48$ phút.

Câu 12 :

Điền số thích hợp vào ô trống:

Vậy độ dài quãng sông AB là

$km$.

Đáp án

Vậy độ dài quãng sông AB là

$km$.

Phương pháp giải :

- Tìm tỉ số giữa thời gian đi xuôi dòng và thời gian đi ngược dòng là $\dfrac{8}{{10}} = \dfrac{4}{5}$.

- Trên cùng một quãng đường thì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch, do đó ta có tỉ lệ giữa vận tốc đi xuôi dòng và vận tốc đi ngược dòng là $\dfrac{5}{4}$.

- Theo đề bài mỗi giờ ca nô đi ngược dòng chậm hơn đi xuôi dòng là $5km$, vậy ta có bài toán tìm hai số khi biết hiệu và tỉ số. Coi vận tốc xuôi dòng là số lớn, vận tốc ngược dòng là số bé. Ta tìm hai số theo công thức:

Số bé $ = $ (hiệu $:$ hiệu số phần bằng nhau) $ \times $ số phần của số bé
Số lớn $ = $ (hiệu $:$ hiệu số phần bằng nhau) $ \times $ số phần của số lớn

- Tìm độ dài quãng sông bằng một trong hai cách:

Độ dài quãng sông $=$ vận tốc xuôi dòng $ \times $ thời gian đi xuôi dòng;

Độ dài quãng sông $=$ vận tốc ngược dòng $ \times $ thời gian đi ngược dòng.

Lời giải chi tiết :

Tỉ số giữa thời gian đi xuôi dòng và thời gian đi ngược dòng là $\dfrac{8}{{10}} = \dfrac{4}{5}$.

Trên cùng một quãng đường thì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch, do đó tỉ lệ giữa vận tốc đi xuôi dòng và vận tốc đi ngược dòng là $\dfrac{5}{4}$.

Ta có sơ đồ:

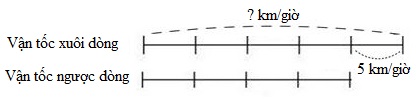
Hiệu số phần bằng nhau là:

$5 - 4 = 1$ (phần)

Vận tốc ca nô khi đi xuôi dòng là:

$5:1 \times 5 = 25$ (km/giờ)

Độ dài quãng sông AB là:

$25 \times 8 = 200\,\,(km)$

Đáp số: $200km$.

Vậy đáp án đúng điền vào ô trống là $200$.

Trắc nghiệm: Hai vật chuyển động cùng chiều Toán 5

Luyện tập và củng cố kiến thức Hai vật chuyển động cùng chiều Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Hai vật chuyển động ngược chiều Toán 5

Luyện tập và củng cố kiến thức Hai vật chuyển động ngược chiều Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Thời gian Toán 5

Luyện tập và củng cố kiến thức Thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Quãng đường Toán 5

Luyện tập và củng cố kiến thức Quãng đường Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Vận tốc Toán 5

Luyện tập và củng cố kiến thức Vận tốc Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Luyện tập về số đo thời gian và các phép tính với số đo thời gian Toán 5

Luyện tập và củng cố kiến thức Luyện tập về số đo thời gian và các phép tính với số đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Chia số đo thời gian cho một số Toán 5

Luyện tập và củng cố kiến thức Chia số đo thời gian cho một số Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Nhân số đo thời gian với một số Toán 5

Luyện tập và củng cố kiến thức Nhân số đo thời gian với một số Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Trừ số đo thời gian Toán 5

Luyện tập và củng cố kiến thức Trừ số đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Cộng số đo thời gian Toán 5

Luyện tập và củng cố kiến thức Cộng số đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Bảng đơn vị đo thời gian Toán 5

Luyện tập và củng cố kiến thức Bảng đơn vị đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Bài giải mới nhất

Trắc nghiệm: Chuyển động trên dòng nước Toán 5

Báo lỗi góp ý