Bài tập trắc nghiệm Toán 5 có đáp án Bài tập trắc nghiệm Chương 4 Số đo thời gian, toán chuy..

Trắc nghiệm: Hai vật chuyển động cùng chiều Toán 5

Làm bài tập

Đề bài

Câu 1 : Con hãy chọn đáp án đúng nhất

Một ô tô đi từ A qua B để đi đến C với vận tốc là ${v_1}$, cùng lúc đó xe máy đi từ B đến C với vận tốc là ${v_2}$. Độ dài quãng đường AB là $s$. Công thức tính thời gian đi để hai xe gặp nhau là:

A. ${t_{gn}} = s:({v_1} + {v_2})$

B. ${t_{gn}} = s:({v_1} - {v_2})$

C. ${t_{gn}} = s:({v_1} \times {v_2})$

D. ${t_{gn}} = s:({v_1}:{v_2})$

Câu 2 : Con hãy chọn đáp án đúng nhất

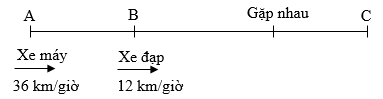
Một người đi xe đạp từ B đến C với vận tốc $12$ km/giờ, cùng lúc đó một người đi xe máy từ A cách B là $60km$ với vận tốc $36$ km/giờ và đuổi theo xe đạp (xem hình vẽ). Hỏi kể từ lúc bắt đầu đi, sau mấy giờ xe máy đuổi kịp xe đạp?

A. $1,25$ giờ

B. $2,5$ giờ

C. $3,5$ giờ

D. $5$ giờ

Câu 3 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống

Điền số thích hợp vào ô trống:

Một ô tô đi từ A đi qua B để đến C với vận tốc $56$ km/giờ. Cùng lúc tại B, một xe máy cũng khởi hành và đi cùng chiều với ô tô với vận tốc bằng $\dfrac{5}{7}$vận tốc ô tô. Biết quãng đường AB dài $48km$.

Vậy kể từ lúc bắt đầu đi, ô tô đuổi kịp xe máy sau

giờ.

Câu 4 : Con hãy chọn đáp án đúng nhất

Lúc $8$ giờ sáng, người thứ I đi từ A đi qua B để đến C với vận tốc $50$km/giờ. Cùng lúc đó tại B, người thứ II cũng khởi hành và đi cùng chiều với người thứ I với vận tốc $12$km/giờ. Biết rằng khoảng cách AB bằng $19km$. Hỏi hai người gặp nhau lúc mấy giờ?

A. $0$ giờ $30$ phút

B. $8$ giờ $16$ phút

C. $8$ giờ $30$ phút

D. $9$ giờ $5$ phút

Câu 5 : Con hãy chọn đáp án đúng nhất

Quân đi xe máy từ A đi qua B để đến C với vận tốc $40$ km/giờ. Cùng lúc đó tại B, Mai đi xe đạp và đi cùng chiều với Quân, với vận tốc $16$ km/giờ. Biết rằng khoảng cách AB bằng $36km$. Hỏi sau bao lâu hai người gặp nhau và địa điểm gặp nhau cách A bao nhiêu ki-lô-mét?

A. $0,64$ giờ; $25,6km$

B. $0,64$ giờ; $46,24km$

C. $1,5$ giờ; $24km$

D. $1,5$ giờ; $60km$

Câu 6 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống

Điền số thích hợp vào ô trống:

Một ô tô đi từ A đuổi theo xe máy đi từ B (hai xe khởi hành cùng một lúc), sau $2$ giờ ô tô đuổi kịp xe máy tại C. Biết vận tốc xe ô tô là 65 km/giờ, vận tốc xe máy là 45 km/giờ.

Vậy độ dài quãng đường AB là

$km$.

Câu 7 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống

Điền số thích hợp vào ô trống:

Một ô tô xuất phát từ A đi qua B để đến C. Cùng lúc đó một xe máy xuất phát từ B cũng đi đến C. Sau $2$ giờ $48$ phút thì ô tô đuổi kịp xe máy. Biết quãng đường AB dài $98km$ và vận tốc ô tô gấp đôi vận tốc xe máy.

Vậy vận tốc của ô tô là

km/giờ; vận tốc xe máy là

km/giờ.

Câu 8 : Con hãy chọn đáp án đúng nhất

Lúc $7$ giờ một ô tô chở hàng đi từ A với vận tốc $48$ km/giờ. Đến $8$ giờ $30$ phút một ô tô du lịch cũng đi từ A với vận tốc $68$ km/giờ và đi cùng chiều với ô tô chở hàng. Tìm thời gian đi để xe ô tô du lịch đuổi kịp xe ô tô chở hàng.

A. $\,0,62$ giờ

B. $\,1,5$ giờ

C. $\,2,75$ giờ

D. $\,3,6$ giờ

Câu 9 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống

Điền số thích hợp vào ô trống:

Một xe máy đi từ A đến B với vận tốc $36$ km/giờ. Sau $1$ giờ $15$ phút, một ô tô cũng đi từ A đến B và đuổi theo xe máy. Sau $1$ giờ $30$ phút, ô tô đuổi kịp xe máy.

Vậy vận tốc ô tô là

km/giờ.

Câu 10 : Con hãy chọn đáp án đúng nhất

Lúc $6$ giờ sáng, một người đi xe đạp từ A đến B với vận tốc $18$ km/giờ. Lúc $8$ giờ, một xe máy đi từ A đến B với vận tốc $45$ km/giờ. Hỏi xe máy đuổi kịp xe đạp vào lúc mấy giờ ? Địa điểm hai xe gặp nhau cách B bao xa? Biết rằng A cách B $115{\rm{ }}km$.

A. $\,9$ giờ $20$ phút; $55km$

B. $\,10$ giờ $20$ phút; $10km$

C. $\,9$ giờ $20$ phút; $60km$

D. $\,10$ giờ $20$ phút; $105km$

Câu 11 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống

Điền số thích hợp vào ô trống:

Một xe máy đi từ A đến B với vận tốc $30$ km/giờ. Khi xe máy đi được $1$ giờ $30$ phút thì một xe ô tô đi với vận tốc $50$ km/h đuổi theo xe máy. Biết $2$ xe cùng đến B lúc $11$ giờ.

Vậy độ dài quãng đường AB là

$km$; xe máy khởi hành lúc

giờ

phút.

Lời giải và đáp án

Câu 1 : Con hãy chọn đáp án đúng nhất

A. ${t_{gn}} = s:({v_1} + {v_2})$

B. ${t_{gn}} = s:({v_1} - {v_2})$

C. ${t_{gn}} = s:({v_1} \times {v_2})$

D. ${t_{gn}} = s:({v_1}:{v_2})$

Đáp án

B. ${t_{gn}} = s:({v_1} - {v_2})$

Phương pháp giải :

Hai vật xuất phát cùng lúc, thời gian đi để gặp nhau bằng quãng đường (khoảng cách ban đầu giữa hai xe) chia cho hiệu hai vận tốc.

Lời giải chi tiết :

Theo đề bài, ô tô và xe máy xuất phát cùng lúc, thời gian đi để gặp nhau bằng quãng đường (khoảng cách ban đầu giữa hai xe) chia cho hiệu hai vận tốc, hay ${t_{gn}} = s:({v_1} - {v_2})$.

Câu 2 : Con hãy chọn đáp án đúng nhất

A. $1,25$ giờ

B. $2,5$ giờ

C. $3,5$ giờ

D. $5$ giờ

Đáp án

B. $2,5$ giờ

Phương pháp giải :

Theo đề bài, xe đạp và xe máy xuất phát cùng lúc. Để giải bài này ta làm như sau:

- Tính hiệu vận tốc hai xe.

- Thời gian đi để gặp nhau bằng khoảng cách ban đầu giữa hai xe chia cho hiệu hai vận tốc.

Lời giải chi tiết :

Hiệu vận tốc của hai xe là:

$36 - 12 = 24$ (km/giờ)

Kể từ lúc bắt đầu đi, xe máy đuổi kịp xe đạp sau số giờ là:

$60:24 = 2,5$ (giờ)

Đáp số: $2,5$ giờ.

Câu 3 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống

Điền số thích hợp vào ô trống:

Vậy kể từ lúc bắt đầu đi, ô tô đuổi kịp xe máy sau

giờ.

Đáp án

Vậy kể từ lúc bắt đầu đi, ô tô đuổi kịp xe máy sau

giờ.

Phương pháp giải :

Theo đề bài, ô tô và xe máy xuất phát cùng lúc. Để giải bài này ta làm như sau:

- Tính vận tốc xe máy ta lấy vận tốc ô tô nhân với $\dfrac{5}{7}$ hoặc lấy vận tốc ô tô chia cho $7$ rồi nhân với $5$.

- Tính hiệu vận tốc hai xe.

- Thời gian đi để gặp nhau bằng khoảng cách ban đầu giữa hai xe chia cho hiệu hai vận tốc.

Lời giải chi tiết :

Vận tốc xe máy là:

$56:7 \times 5 = 40$ (km/giờ)

Hiệu vận tốc của hai xe là:

$56 - 40 = 16$ (km/giờ)

Kể từ lúc bắt đầu đi, ô tô đuổi kịp xe đạp sau số giờ là:

$48:16 = 3$ (giờ)

Đáp số: $3$ giờ.

Vậy đáp án đúng điền vào ô trống là $3$.

Câu 4 : Con hãy chọn đáp án đúng nhất

A. $0$ giờ $30$ phút

B. $8$ giờ $16$ phút

C. $8$ giờ $30$ phút

D. $9$ giờ $5$ phút

Đáp án

C. $8$ giờ $30$ phút

Phương pháp giải :

Theo đề bài, hai người xuất phát cùng lúc. Để giải bài này ta làm như sau:

- Tính hiệu vận tốc của hai người.

- Thời gian đi để gặp nhau bằng khoảng cách ban đầu giữa hai người chia cho hiệu hai vận tốc.

- Đổi số đo thời gian dạng số thập phân sang dạng số tự nhiên.

- Thời gian lúc hai người gặp nhau = thời gian xuất phát + thời gian đi để gặp nhau.

Lời giải chi tiết :

Hiệu vận tốc của hai người là:

$50 - 12 = 38$ (km/giờ)

Thời gian đi để hai người gặp nhau là:

$19:38 = 0,5$ (giờ)

Đổi: $0,5$ giờ $ = \,\,30$ phút

Hai người gặp nhau lúc:

$8$ giờ $ + \,\,30$ phút $ = \,\,8$ giờ $30$ phút

Đáp số: $8$ giờ $30$ phút

Câu 5 : Con hãy chọn đáp án đúng nhất

A. $0,64$ giờ; $25,6km$

B. $0,64$ giờ; $46,24km$

C. $1,5$ giờ; $24km$

D. $1,5$ giờ; $60km$

Đáp án

D. $1,5$ giờ; $60km$

Phương pháp giải :

Theo đề bài, hai người xuất phát cùng lúc. Để giải bài này ta làm như sau:

- Tính hiệu vận tốc của Quân và Mai.

- Thời gian đi để gặp nhau bằng khoảng cách ban đầu giữa hai xe chia cho hiệu hai vận tốc.

- Khoảng cách từ chỗ gặp nhau đến A chính là quãng đường mà Quân đã đi từ lúc xuất phát đến lúc gặp nhau. Để tính quãng đường đó ta lấy vận tốc của Quân nhân với thời gian đi để gặp nhau.

Lời giải chi tiết :

Hiệu vận tốc của Quân và Mai là:

$40 - 16 = 24$ (km/giờ)

Thời gian đi để hai người gặp nhau là:

$36:24 = 1,5$ (giờ)

Địa điểm gặp nhau cách A số ki-lô-mét là:

$40 \times 1,5 = 60\;(km)$

Đáp số: $1,5$ giờ; $60km$.

Câu 6 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống

Điền số thích hợp vào ô trống:

Vậy độ dài quãng đường AB là

$km$.

Đáp án

Vậy độ dài quãng đường AB là

$km$.

Phương pháp giải :

Theo đề bài, ô tô và xe máy xuất phát cùng lúc. Để giải bài này ta làm như sau:

- Tính hiệu vận tốc hai xe.

- Tính quãng đường AB ta lấy hiệu hai vận tốc nhân với thời gian đi để gặp nhau.

Lời giải chi tiết :

Hiệu vận tốc hai xe là:

$65 - 45 = 20$ (km/giờ)

Quãng đường AB dài số ki-lô-mét là:

$20 \times 2 = 40\;(km)$

Đáp số: $40km$.

Vậy đáp án đúng điền vào ô trống là $40$.

Câu 7 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống

Điền số thích hợp vào ô trống:

Vậy vận tốc của ô tô là

km/giờ; vận tốc xe máy là

km/giờ.

Đáp án

Vậy vận tốc của ô tô là

km/giờ; vận tốc xe máy là

km/giờ.

Phương pháp giải :

Theo đề bài, hai ô tô xuất phát cùng lúc. Để giải bài này ta làm như sau:

- Đổi số đo thời gian sang dạng số thập phân có đơn vị là giờ.

- Tính hiệu vận tốc hai ô tô ta lấy quãng đường chia cho thời gian đi để gặp nhau.

- Khi đó ta có bài toán tìm hai số khi biết hiệu và tỉ số. Theo đề bài, vận tốc ô tô gấp đôi vận tốc xe máy nên ta vẽ sơ đồ biểu thị vận tốc xe máy là $1$ phần thì vận tốc ô tô là $2$ phần như thế. Coi vận tốc xe máy là số bé, vận tốc ô tô là số lớn, ta tìm hai số theo công thức:

Số bé = Giá trị một phần × số phần của số bé

hoặc

Số lớn = Giá trị một phần × số phần của số lớn.

Lời giải chi tiết :

Đổi $2$ giờ $48$ phút $ = \,2,8$ giờ

Hiệu vận tốc hai xe là:

$98:2,8 = 35$ (km/giờ)

Ta có sơ đồ:

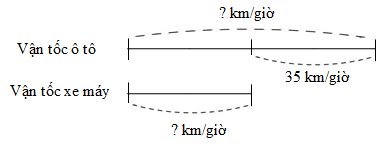
Hiệu số phần bằng nhau là:

$2 - 1 = 1$ (phần)

Giá trị một phần hay vận tốc xe máy là:

$35:1 \times 1 = 35$ (km/giờ)

Vận tốc ô tô là

$35 \times 2 = 70$ (km/giờ)

Đáp số: Vận tốc ô tô: $70$ km/giờ;

Vận tốc xe máy: $35$ km/giờ.

Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là $70\,;\,\,35$.

Câu 8 : Con hãy chọn đáp án đúng nhất

A. $\,0,62$ giờ

B. $\,1,5$ giờ

C. $\,2,75$ giờ

D. $\,3,6$ giờ

Đáp án

D. $\,3,6$ giờ

Phương pháp giải :

Theo đề bài, hai ô tô xuất phát không cùng lúc. Đến $8$ giờ $30$ phút thì hai xe mới cùng chuyển động. Để giải bài này ta làm như sau:

- Tính thời gian ô tô chở hàng đi trước ô tô du lịch: $8$ giờ $30$ phút $ - \,7$ giờ $ = \,1$ giờ $30$ phút và đổi kết quả vừa tìm được sang dạng số thập phân có đơn vị là giờ.

- Tìm quãng đường xe ô tô chở hàng đã đi trước khi ô tô du lich xuất phát (hay khoảng cách giữa hai xe khi ô tô du lịch xuất phát) ta lấy vận tốc ô tô chở hàng nhân với thời gian ô tô chở hàng đi trước ô tô du lịch.

- Tìm hiệu vận tốc hai xe.

- Tìm thời gian đi để xe ô tô du lịch đuổi kịp xe ô tô chở hàng ta lấy khoảng cách giữa hai xe khi ô tô du lịch xuất phát chia cho hiệu vận tốc.

Lời giải chi tiết :

Thời gian ô tô chở hàng đi trước ô tô du lịch là:

$8$ giờ $30$ phút $ - \,7$ giờ $ = \,1$ giờ $30$ phút

Đổi $1$ giờ $30$ phút $ = \,1,5$ giờ

Quãng đường xe ô tô chở hàng đã đi trước khi ô tô du lich xuất phát (hay khoảng cách giữa hai xe khi ô tô du lịch xuất phát) là:

$48 \times 1,5 = 72 \;(km)$

Hiệu vận tốc hai ô tô là:

$68 - 48 = 20$ (km/giờ)

Thời gian đi để xe ô tô du lịch đuổi kịp xe ô tô chở hàng là:

$72:20 = 3,6$ (giờ)

Đáp số: $\,3,6$ giờ.

Câu 9 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống

Điền số thích hợp vào ô trống:

Vậy vận tốc ô tô là

km/giờ.

Đáp án

Vậy vận tốc ô tô là

km/giờ.

Phương pháp giải :

Theo đề bài, xe đạp và xe máy xuất phát không cùng lúc. Sau khi xe máy đã đi được $1$ giờ $15$ phút thì hai xe mới cùng chuyển động. Để giải bài này ta làm như sau:

- Đổi $1$ giờ $15$ phút và $1$ giờ $30$ phút sang dạng số thập phân có đơn vị là giờ.

- Tính quãng đường xe máy đi được trước khi ô tô xuất phát (hay khoảng cách giữa hai xe) ta lấy vận tốc xe máy nhân với thời gian xe máy đi trước ô tô.

- Tính hiệu vận tốc hai xe ta lấy quãng đường xe máy đi được trước khi ô tô xuất phát chia cho thời gian để ô tô đuổi kịp xe máy.

- Tìm vận tốc ô tô ta lấy vận tốc xe máy cộng với hiệu vận tốc hai xe.

Lời giải chi tiết :

Đổi: $1$ giờ $15$ phút $ = 1,25$ giờ ; $1$ giờ $30$ phút $ = 1,5$ giờ.

Quãng đường xe máy đi được trước khi ô tô xuất phát (hay khoảng cách giữa hai xe) là:

$36 \times 1,25 = 45 \;(km)$

Hiệu vận tốc hai xe là:

$45:1,5 = 30$ km/giờ)

Vận tốc ô tô là:

$36 + 30 = 66$ (km/giờ)

Đáp số: $66$ km/giờ.

Vậy đáp án đúng điền vào ô trống là $66$.

Câu 10 : Con hãy chọn đáp án đúng nhất

A. $\,9$ giờ $20$ phút; $55km$

B. $\,10$ giờ $20$ phút; $10km$

C. $\,9$ giờ $20$ phút; $60km$

D. $\,10$ giờ $20$ phút; $105km$

Đáp án

A. $\,9$ giờ $20$ phút; $55km$

Phương pháp giải :

Theo đề bài, xe đạp và xe máy xuất phát không cùng lúc. Đến $8$ giờ thì hai xe mới cùng chuyển động. Để giải bài này ta làm như sau:

- Tính thời gian xe đạp đi trước xe máy.

- Tìm quãng đường xe đạp đã đi trước khi xe máy xuất phát (hay khoảng cách giữa hai xe khi xe máy xuất phát) ta lấy vận tốc xe đạp nhân với thời gian xe đạp đi trước xe máy.

- Tìm hiệu vận tốc hai xe.

- Tìm thời gian đi để xe máy đuổi kịp xe đạp ta lấy khoảng cách giữa hai xe khi xe máy xuất phát chia cho hiệu vận tốc.

- Đổi số đo thời gian vừa tìm được sang số tự nhiên.

- Thời gian lúc xe máy đuổi kịp xe đạp = thời gian xuất phát của xe máy + thời gian đi để xe máy đuổi kịp xe đạp.

- Nếu số phút ở kết quả lớn hơn hoặc bằng $60$ thì ta thực hiện chuyển đổi sang đơn vị lớn hơn phút là giờ.

- Tìm khoảng cách giữa điểm hai xe gặp nhau và B (đoạn đường BC) ta lấy độ dài quãng đường AB trừ đi khoảng cách từ A đến điểm hai xe gặp nhau (khoảng cách A đến điểm hai xe gặp nhau chính là quãng đường xe máy đi từ lúc xuất phát đến lúc gặp nhau, là đoạn đường AC).

Lời giải chi tiết :

Ta có sơ đồ chuyển động của hai xe như sau:

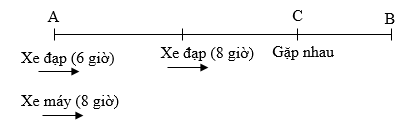
Thời gian xe đạp đi trước xe máy là:

$8$ giờ $ - \,6$ giờ $ = \,2$ giờ

Quãng đường xe đạp đã đi trước khi xe máy xuất phát (hay khoảng cách giữa hai xe khi xe máy xuất phát) là:

$18 \times 2 = 36\;(km)$

Hiệu vận tốc hai xe là:

$45 - 18 = 27$ (km/giờ)

Thời gian đi để xe máy đuổi kịp xe đạp là:

$36:27 = \dfrac{4}{3}$ (giờ)

Đổi $\dfrac{4}{3}$ giờ $ = \,1\dfrac{1}{3}$ giờ $ = \,\,1$ giờ $20$ phút

Xe máy đuổi kịp xe đạp lúc:

$8$ giờ $ + \,1$ giờ $20$ phút $ = \,9$ giờ $20$ phút

Địa điểm gặp nhau cách A số ki-lô-mét là:

$45 \times \dfrac{4}{3} = 60\;(km)$

Địa điểm gặp nhau cách B số ki-lô-mét là:

$115 - 60 = 55\;(km)$

Đáp số: $\,9$ giờ $20$ phút; $55km$.

Câu 11 : Con hãy điền từ/cụm từ/số thích hợp vào các ô trống

Điền số thích hợp vào ô trống:

Vậy độ dài quãng đường AB là

$km$; xe máy khởi hành lúc

giờ

phút.

Đáp án

Vậy độ dài quãng đường AB là

$km$; xe máy khởi hành lúc

giờ

phút.

Phương pháp giải :

Theo đề bài, ô tô và xe máy xuất phát không cùng lúc. Sau khi xe máy đã đi được $1$ giờ $30$ phút thì hai xe mới cùng chuyển động. Để giải bài này ta làm như sau:

- Đổi số đo thời gian sang dạng số thập phân có đơn vị là giờ.

- Tìm quãng đường xe máy đã đi trước khi ô tô xuất phát (hay khoảng cách giữa hai xe khi ô tô xuất phát) ta lấy vận tốc xe máy nhân với thời gian xe máy đi trước ô tô.

- Tìm hiệu vận tốc hai xe.

- Tìm thời gian đi để hai xe gặp nhau ta lấy quãng đường xe máy đã đi trước khi ô tô xuất phát chia cho hiệu vận tốc hai xe.

- Độ dài quãng đường AB bằng quãng đường ô tô đã đi, ta lấy vận tốc ô tô nhân với thời gian đi để hai xe gặp nhau tại B.

- Tìm thời gian xe máy khởi hành = Thời gian lúc xe đến B – thời gian đi để hai xe gặp nhau – thời gian xe máy đi trước ô tô.

Lời giải chi tiết :

Đổi $1$ giờ $30$ phút $ = 1,5$ giờ

Quãng đường xe máy đã đi trước khi ô tô xuất phát (hay khoảng cách giữa hai xe khi ô tô xuất phát) là:

$30 \times 1,5 = 45 \;(km)$

Hiệu vận tốc hai xe là:

$50 - 30 = 20$ (km/giờ)

Thời gian đi để hai xe gặp nhau là:

$45:20 = 2,25$ (giờ)

Đổi $2,25$ giờ $ = \,\,2$ giờ $15$ phút

Độ dài quãng đường AB là:

$50 \times 2,25 = 112,5 \;(km)$

Xe máy khởi hành lúc:

$11$ giờ $ - \,2$ giờ $15$ phút $ - \,1$ giờ $30$ phút $ = \,7$ giờ $15$ phút

Đáp số: $112,5km\,;\,\,7$ giờ $15$ phút.

Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là $112,5\,;\,\,7\,;\,\,15$.

Trắc nghiệm: Chuyển động trên dòng nước Toán 5

Luyện tập và củng cố kiến thức Chuyển động trên dòng nước Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Hai vật chuyển động ngược chiều Toán 5

Luyện tập và củng cố kiến thức Hai vật chuyển động ngược chiều Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Thời gian Toán 5

Luyện tập và củng cố kiến thức Thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Quãng đường Toán 5

Luyện tập và củng cố kiến thức Quãng đường Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Vận tốc Toán 5

Luyện tập và củng cố kiến thức Vận tốc Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Luyện tập về số đo thời gian và các phép tính với số đo thời gian Toán 5

Luyện tập và củng cố kiến thức Luyện tập về số đo thời gian và các phép tính với số đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Chia số đo thời gian cho một số Toán 5

Luyện tập và củng cố kiến thức Chia số đo thời gian cho một số Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Nhân số đo thời gian với một số Toán 5

Luyện tập và củng cố kiến thức Nhân số đo thời gian với một số Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Trừ số đo thời gian Toán 5

Luyện tập và củng cố kiến thức Trừ số đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Cộng số đo thời gian Toán 5

Luyện tập và củng cố kiến thức Cộng số đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Bảng đơn vị đo thời gian Toán 5

Luyện tập và củng cố kiến thức Bảng đơn vị đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Hai vật chuyển động cùng chiều Toán 5

Bài giải mới nhất

Báo lỗi góp ý