Trắc nghiệm: Hình thang. Diện tích hình thang Toán 5
Đề bài
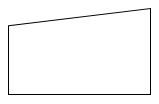
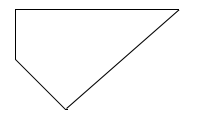
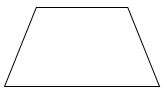
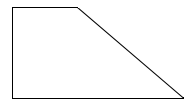
 Trong các hình sau, hình nào là hình thang?
Trong các hình sau, hình nào là hình thang?

Một hình thang có đáy lớn là \(a\), đáy bé là \(b\), chiều cao là \(h\). Khi đó công thức tính diện tích hình thang đó là:
A. \((a + b) \times h\, \times 2\) \(\)
B. \(\dfrac{{(a - b) \times h}}{2}\)
C. \(\dfrac{{(a + b) \times h}}{2}\)
D. \(\dfrac{{a + b\, \times h}}{2}\)

Tính diện tích hình thang biết độ dài hai đáy là \(17cm\) và \(12cm\), chiều cao là \(8cm\).
A. \(40c{m^2}\)
B. \(58c{m^2}\)
C. \(116c{m^2}\)
D. \(232c{m^2}\)
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Diện tích hình thang có đáy lớn là \(45dm\), đáy bé là \(25dm\) và chiều cao là \(2m\) là
\(d{m^2}\).

Điền số thích hợp vào ô trống:
Cho hình thang như hình vẽ:
Diện tích hình thang đã cho là
\(c{m^2}\).

Hình thang $ABCD$ có chiều cao $AH$ bằng $75cm$; đáy bé bằng $\dfrac{2}{3}$ đáy lớn. Biết diện tích hình thang bằng diện tích hình chữ nhật có chiều dài $135cm$; chiều rộng $50cm$. Tính độ dài đáy lớn, đáy bé của hình thang.
A. Đáy lớn \(54cm\) ; đáy bé \(36cm\)
B. Đáy lớn \(90cm\) ; đáy bé \(60cm\)
C. Đáy lớn \(72cm\) ; đáy bé \(48cm\)
D. Đáy lớn \(108cm\) ; đáy bé \(72cm\)

Điền số thích hợp vào ô trống:
Trung bình cộng hai đáy hình thang là $17,5m$. Biết đáy lớn hơn đáy bé $13m$. Chiều cao bằng \(\dfrac{3}{4}\) đáy lớn.
Vậy diện tích hình thang đó là
\({m^2}.\)

Điền số thích hợp vào chỗ trống:
Cho hình chữ nhật $ABCD$ có $AB = 24,4cm\;;{\rm{ }}BC = 11cm\;$.
Điểm \(M\) nằm trên cạnh $AB$ sao cho$AM = \dfrac{3}{5}AB$.
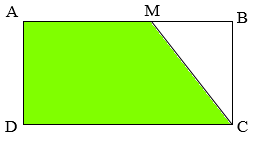
Diện tích hình thang $AMCD$ là
\(c{m^2}\)

Điền số thích hợp vào ô trống:
Cho hình thang \(ABCD\) có diện tích là $9,18{m^2}$ ; đáy bé $AB = 1,7m$; đáy lớn \(CD\) gấp hai lần đáy bé \(AB\).
Vậy chiều cao \(AH\) là
\(m.\)
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Một mảnh vườn hình thang có chiều cao $22m$; đáy bé bằng $17,5m$ và kém đáy lớn \(9m\).
Người ta dự định dùng $\dfrac{1}{4}$ diện tích đất để trồng xoài, diện tích còn lại dùng để trồng cam.
Vậy diện tích đất trồng cam là
\({m^2}\)

Một thửa ruộng hình thang có đáy bé bằng \(\dfrac{3}{5}\) đáy lớn, chiều cao bằng $\dfrac{1}{4}$ đáy lớn. Biết đáy lớn hình thang là $260m$. Để làm sạch cỏ trên thửa ruộng, bác Hùng cần $0,75$ giờ cho mỗi $100{m^2}$ đất. Hỏi bác Hùng cần dùng bao nhiêu giờ để làm sạch cỏ trên cả thửa ruộng ấy?
A. \(76,05\) giờ
B. \(101,4\) giờ
C. \(180\) giờ
D. \(202,8\) giờ

Điền số thích hợp vào ô trống:
Cho hình thang có độ dài hai đáy lần lượt là $15,6m$ và $9,5m$.
Nếu kéo dài đáy lớn thêm $1,75m$ thì diện tích tăng thêm $7{m^2}.$
Vậy diện tích hình thang ban đầu là
\(d{m^2}\).
Lời giải và đáp án
 Trong các hình sau, hình nào là hình thang?
Trong các hình sau, hình nào là hình thang?







Quan sát hình vẽ và áp dụng tính chất hình thang có một cặp cạnh đối diện song song.
Quan sát các hình đã cho ta thấy các hình thứ nhất, thứ ba và thứ tư có một cặp cạnh đối diện song song nên các hình đó là hình thang.

Một hình thang có đáy lớn là \(a\), đáy bé là \(b\), chiều cao là \(h\). Khi đó công thức tính diện tích hình thang đó là:
A. \((a + b) \times h\, \times 2\) \(\)
B. \(\dfrac{{(a - b) \times h}}{2}\)
C. \(\dfrac{{(a + b) \times h}}{2}\)
D. \(\dfrac{{a + b\, \times h}}{2}\)
C. \(\dfrac{{(a + b) \times h}}{2}\)
Dựa vào cách tính diện tích hình thang: Muốn tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho \(2\).
Muốn tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho \(2\).
Do đó, hình thang có đáy lớn là \(a\), đáy bé là \(b\), chiều cao là \(h\) thì diện tích hình thang đó được tính theo công thức:
\(\dfrac{{(a + b) \times h}}{2}\).

Tính diện tích hình thang biết độ dài hai đáy là \(17cm\) và \(12cm\), chiều cao là \(8cm\).
A. \(40c{m^2}\)
B. \(58c{m^2}\)
C. \(116c{m^2}\)
D. \(232c{m^2}\)
C. \(116c{m^2}\)
Độ dài hai đáy và chiều cao đã có cùng đơn vị đo nên để tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho \(2\).
Diện tích hình thang đó là:
\(\dfrac{{(17 + 12) \times 8}}{2} = 116\left( {c{m^2}} \right)\)
Đáp số: \(116c{m^2}\)
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Diện tích hình thang có đáy lớn là \(45dm\), đáy bé là \(25dm\) và chiều cao là \(2m\) là
\(d{m^2}\).
Diện tích hình thang có đáy lớn là \(45dm\), đáy bé là \(25dm\) và chiều cao là \(2m\) là
\(d{m^2}\).
Chiều cao chưa cùng đơn vị đo với hai đáy nên ta đổi về cùng đơn vị đo \(2m = 20dm\), sau đó tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho \(2\).
Đổi \(2m = 20dm\)
Diện tích hình thang đó là:
\(\dfrac{{(45 + 25) \times 20}}{2} = 700\left( {d{m^2}} \right)\)
Đáp số: \(700d{m^2}\)
Vậy đáp án đúng điền vào ô trống là \(700\).

Điền số thích hợp vào ô trống:
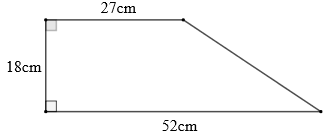
Cho hình thang như hình vẽ:

Diện tích hình thang đã cho là
\(c{m^2}\).
Cho hình thang như hình vẽ:

Diện tích hình thang đã cho là
\(c{m^2}\).
Hình thang đã cho là hình thang vuông có chiều cao là \(18cm\), độ dài hai đáy là \(27cm\) và \(52cm\). Để tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho \(2\).
Diện tích hình thang đó là:
\(\dfrac{{(27 + 52) \times 18}}{2} = 711\left( {c{m^2}} \right)\)
Đáp số: \(711c{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(711\).

Hình thang $ABCD$ có chiều cao $AH$ bằng $75cm$; đáy bé bằng $\dfrac{2}{3}$ đáy lớn. Biết diện tích hình thang bằng diện tích hình chữ nhật có chiều dài $135cm$; chiều rộng $50cm$. Tính độ dài đáy lớn, đáy bé của hình thang.
A. Đáy lớn \(54cm\) ; đáy bé \(36cm\)
B. Đáy lớn \(90cm\) ; đáy bé \(60cm\)
C. Đáy lớn \(72cm\) ; đáy bé \(48cm\)
D. Đáy lớn \(108cm\) ; đáy bé \(72cm\)
D. Đáy lớn \(108cm\) ; đáy bé \(72cm\)
- Tính diện tích hình chữ nhật theo công thức: Diện tích = chiều dài × chiều rộng.
Từ đó tìm được diện tích hình thang.
- Từ công thức tính diện tích \(S = \dfrac{{(a + b) \times h}}{2}\) ta có thể tính tổng độ dài hai đáy \(h\) theo công thức \(a + b = \dfrac{{S \times 2}}{h}\) hoặc \(a + b = S \times 2:h\).
Khi đó ta có bài toán tổng tỉ cơ bản, giải bài toán ta tìm được đáy lớn, đáy bé.
Diện tích hình chữ nhật là:
\(135 \times 50 = 6750\;(c{m^2})\)
Vậy hình thang có diện tích là \(6750c{m^2}\).
Tổng độ dài hai đáy của hình thang là:
\(6750 \times 2:75 = 180\;(cm)\)
Ta có sơ đồ
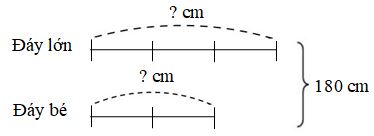
Theo sơ đồ, tổng số phần bằng nhau là:
\(2 + 3 = 5\) (phần)
Giá trị một phần là:
\(180:5 = 36\;(cm)\)
Độ dài đáy lớn là:
\(36 \times 3 = 108\;(cm)\)
Độ dài đáy bé là:
\(180 - 108 = 72\;(cm)\)
Đáp số: Đáy lớn \(108cm\) ; đáy bé \(72cm\).
Học sinh cần xác định đúng công thức tính tổng độ dài hai đáy, một số học sinh tính tổng độ dài hai đáy bằng cách lấy diện tích chia cho chiều cao nên kết quả chưa đúng.

Điền số thích hợp vào ô trống:
Trung bình cộng hai đáy hình thang là $17,5m$. Biết đáy lớn hơn đáy bé $13m$. Chiều cao bằng \(\dfrac{3}{4}\) đáy lớn.
Vậy diện tích hình thang đó là
\({m^2}.\)
Trung bình cộng hai đáy hình thang là $17,5m$. Biết đáy lớn hơn đáy bé $13m$. Chiều cao bằng \(\dfrac{3}{4}\) đáy lớn.
Vậy diện tích hình thang đó là
\({m^2}.\)
Muốn tính được diện tích hình thang ta phải biết độ dài hai đáy và chiều cao. Ta có thể giải bài này như sau:
- Tính tổng độ dài hai đáy ta lấy trung bình cộng nhân với \(2\). Khi đó ta có bài toán tìm hai số khi biết tổng và hiệu của hai số. Ta tìm độ dài hai đáy theo công thức:
Số lớn = (tổng + hiệu) \(:2\) ; Số bé = (tổng – hiệu) \(:2\)
- Tìm chiều cao ta lấy đáy lớn nhân với \(\dfrac{3}{4}\).
- Tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho \(2\).
Tổng độ dài hai đáy của hình thang là:
$17,5 \times 2 = 35\;(m)$
Độ dài đáy lớn của hình thang là:
$(35 + 13):2 = 24\;(m)$
Độ dài đáy bé của hình thang là:
$35 - 24 = 11\;(m)$
Chiều cao của hình thang là:
$24 \times \dfrac{3}{4} = 18\;(m)$
Diện tích của hình thang là:
$(24 + 11) \times 18:2 = 315\;({m^2})$
Đáp số: \(315{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(315\).
Học sinh cần nhớ công thức tính tổng khi biết trung bình cộng và cách tìm hai số khi biết tổng và hiệu của hai số đó.

Điền số thích hợp vào chỗ trống:
Cho hình chữ nhật $ABCD$ có $AB = 24,4cm\;;{\rm{ }}BC = 11cm\;$.
Điểm \(M\) nằm trên cạnh $AB$ sao cho$AM = \dfrac{3}{5}AB$.

Diện tích hình thang $AMCD$ là
\(c{m^2}\)
Cho hình chữ nhật $ABCD$ có $AB = 24,4cm\;;{\rm{ }}BC = 11cm\;$.
Điểm \(M\) nằm trên cạnh $AB$ sao cho$AM = \dfrac{3}{5}AB$.

Diện tích hình thang $AMCD$ là
\(c{m^2}\)
- $ABCD$ là hình chữ nhật nên $AB = CD = 24,4cm;\,\,AD = BC = 11cm$
- Tính độ dài cạnh \(AM\) ta lấy độ dài cạnh \(AB\) nhân với \(\dfrac{3}{5}\).
- Hình thang $AMCD$ có chiều cao chính là cạnh \(AD\), từ đó tính diện tích hình thang theo công thức:
\(S = (AM + CD) \times AD:2\).
Vì $ABCD$ là hình chữ nhật nên $AB = CD = 24,4cm;\,\,AD = BC = 11cm$.
Hình thang $AMCD$ có chiều cao là \(AD = 11cm\).
Độ dài cạnh \(AM\) là:
\(24,4 \times \dfrac{3}{5} = 14,64\;(cm)\)
Diện tích hình thang $AMCD$ là:
\(\dfrac{{(14,64 + 24,4) \times 11}}{2} = 214,72\;\left( {c{m^2}} \right)\)
Đáp số: \(214,72c{m^2}\).

Điền số thích hợp vào ô trống:
Cho hình thang \(ABCD\) có diện tích là $9,18{m^2}$ ; đáy bé $AB = 1,7m$; đáy lớn \(CD\) gấp hai lần đáy bé \(AB\).
Vậy chiều cao \(AH\) là
\(m.\)
Cho hình thang \(ABCD\) có diện tích là $9,18{m^2}$ ; đáy bé $AB = 1,7m$; đáy lớn \(CD\) gấp hai lần đáy bé \(AB\).
Vậy chiều cao \(AH\) là
\(m.\)
- Tính độ dài đáy lớn ta lấy độ dài đáy bé nhân với \(2\).
- Từ công thức tính diện tích \(S = \dfrac{{(a + b) \times h}}{2}\) ta có thể tính chiều cao \(h\) theo công thức \(h = \dfrac{{S\,\, \times \,\,2}}{{(a + b)}}\) hoặc \(h = S \times 2:(a + b)\).
Độ dài đáy lớn \(CD\) là:
\(1,7 \times 2 = 3,4\;(cm)\)
Chiều cao \(AH\) dài là:
\(9,18 \times 2:(1,7 + 3,4) = 3,6\;(m)\)
Đáp số: \(3,6m\).
Vậy đáp án đúng điền vào ô trống là \(3,6\).
Học sinh cần xác định đúng công thức tính chiều cao, một số học sinh tính chiều cao bằng cách lấy diện tích chia cho tổng độ dài hai đáy nên kết quả chưa đúng.
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Một mảnh vườn hình thang có chiều cao $22m$; đáy bé bằng $17,5m$ và kém đáy lớn \(9m\).
Người ta dự định dùng $\dfrac{1}{4}$ diện tích đất để trồng xoài, diện tích còn lại dùng để trồng cam.
Vậy diện tích đất trồng cam là
\({m^2}\)
Một mảnh vườn hình thang có chiều cao $22m$; đáy bé bằng $17,5m$ và kém đáy lớn \(9m\).
Người ta dự định dùng $\dfrac{1}{4}$ diện tích đất để trồng xoài, diện tích còn lại dùng để trồng cam.
Vậy diện tích đất trồng cam là
\({m^2}\)
- Đáy bé kém đáy lớn \(9m\) tức là đáy lớn hơn đáy bé \(9m\). Để tính độ dài đáy lớn ta lấy đáy bé cộng với \(9m\).
- Tính diện tích cả mảnh vườn ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho \(2\).
- Tính diện tích đất để trồng xoài ta lấy diện tích cả mảnh vườn nhân với \(\dfrac{1}{4}\) .
- Tính diện tích đất để trồng cam ta lấy diện tích cả mảnh vườn trừ đi diện tích đất để trồng xoài.
Độ dài đáy lớn của mảnh vườn là:
$17,5 + 9 = 26,5\;(m)$
Diện tích mảnh vườn đó là:
$(17,5 + 26,5) \times 22:2 = 484\;({m^2})$
Diện tích đất để trồng xoài là:
$484 \times \dfrac{1}{4} = 121\;({m^2})$
Diện tích đất để trồng cam là:
$484 - 121 = 363\;({m^2})$
Đáp số: \(363{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(363\).

Một thửa ruộng hình thang có đáy bé bằng \(\dfrac{3}{5}\) đáy lớn, chiều cao bằng $\dfrac{1}{4}$ đáy lớn. Biết đáy lớn hình thang là $260m$. Để làm sạch cỏ trên thửa ruộng, bác Hùng cần $0,75$ giờ cho mỗi $100{m^2}$ đất. Hỏi bác Hùng cần dùng bao nhiêu giờ để làm sạch cỏ trên cả thửa ruộng ấy?
A. \(76,05\) giờ
B. \(101,4\) giờ
C. \(180\) giờ
D. \(202,8\) giờ
B. \(101,4\) giờ
- Tìm đáy lớn và chiều cao theo quy tắc: muốn tìm phân số của một số ta lấy số đó nhân với phân số.
- Tìm diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho \(2\).
- Tìm số giờ để làm sạch cỏ theo bài toán tỉ lệ thuận: tìm tỉ số giữa diện tích và \(100m^2\), diện tích gấp \(100m^2\) bao nhiêu lần thì số giờ để làm sạch cỏ cũng gấp \(0,75\) giờ bấy nhiêu lần.
Độ dài đáy bé của thửa ruộng đó là:
$260 \times \dfrac{3}{5} = 156\;(m)$
Chiều cao của thửa ruộng đó là:
$260 \times \dfrac{1}{4} = 65\;(m)$
Diện tích của thửa ruộng đó là:
$\dfrac{{(156 + 260) \times 65}}{2} = 13520\;({m^2})$
$13520{m^2}$ gấp $100{m^2}$ số lần là:
$13520:100 = 135,2$ (lần)
Bác Hùng cần dùng số giờ để làm sạch cỏ trên cả thửa ruộng đó là:
\(0,75 \times 135,2 = 101,4\) (giờ)
Đáp số: \(101,4\) giờ.
- Học sinh cần nhớ cách tìm phân số của một số.
- Bước cuối tìm số giờ cần để làm sạch cỏ ta có thể làm gộp thành một bước: \(13520:100 \times 0,75\)

Điền số thích hợp vào ô trống:
Cho hình thang có độ dài hai đáy lần lượt là $15,6m$ và $9,5m$.
Nếu kéo dài đáy lớn thêm $1,75m$ thì diện tích tăng thêm $7{m^2}.$
Vậy diện tích hình thang ban đầu là
\(d{m^2}\).
Cho hình thang có độ dài hai đáy lần lượt là $15,6m$ và $9,5m$.
Nếu kéo dài đáy lớn thêm $1,75m$ thì diện tích tăng thêm $7{m^2}.$
Vậy diện tích hình thang ban đầu là
\(d{m^2}\).
- Vẽ hình theo đề bài ta thấy diện tích phần tăng thêm là diện tích tam giác có đáy là \(1,75m\) và chiều cao chính là chiều cao của hình thang, từ đó áp dụng công thức \(h = S \times 2:a\) ta tìm được chiều cao .
- Tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho \(2\).
- Đổi diện tích ra đơn vị đề bài yêu cầu là \(d{m^2}\).
Theo bài ra ta có hình vẽ:
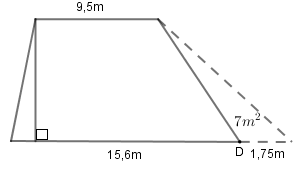
Phần diện tích tăng thêm chính là diện tích của hình tam giác có đáy là $1,75m$ và chiều cao cũng chính là chiều cao của hình thang.
Chiều cao của hình thang là:
\(7 \times 2:1,75 = 8\;(m)\)
Diện tích hình thang là:
\((15,6 + 9,5) \times 8:2 = 100,4\;\left( {{m^2}} \right)\)
\(100,4{m^2} = 10040d{m^2}\)
Đáp số: \(10040d{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(10040\).
Với những dạng bài này, học sinh cần vẽ hình để xác định được được phần tăng thêm cũng như xác định chiều cao tương ứng với các cạnh của tam giác và chiều cao của hình thang.
Luyện tập và củng cố kiến thức Hình tròn. Đường tròn. Chu vi hình tròn Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Diện tích hình tròn Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Luyện tập về diện tích các hình Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Hình hộp chữ nhật. Hình lập phương Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Diện tích xung quanh và diện tích toàn phần của hình lập phương Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Thể tích của một hình. Xăng-ti-mét khối. Đề-xi-mét khối. Mét khối Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Thể tích hình hộp chữ nhật Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Thể tích hình lập phương Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập chương 3 Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Hình tam giác. Diện tích hình tam giác Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết










Danh sách bình luận