Bài tập trắc nghiệm Toán 5 có đáp án Bài tập trắc nghiệm Chương 4 Số đo thời gian, toán chuy..

Trắc nghiệm: Nhân số đo thời gian với một số Toán 5

Đề bài

Xem đáp án

Làm bài tập

Đề bài

Câu 1 :

Điền số thích hợp vào ô trống:

$1,2$ giờ =

phút.

Câu 2 :

Điền số thích hợp vào ô trống:

$8,4$ thế kỉ =

năm.

Câu 3 :

Cho phép tính như sau:

Số thích hợp điền vào ô trống theo thứ tự từ trái sang phải lần lượt là:

A. $6;\,\,45$.

B. $6;\,\,15$.

C. $8;\,\,45$.

D. $8;\,\,15$.

Câu 4 :

Tính: $4$ năm $5$ tháng $ \times \,5$.

A. $4$ năm $25$ tháng

B. $20$ năm $5$ tháng

C. $22$ năm $1$ tháng

D. $22$ năm $5$ tháng

Câu 5 :

$2$ ngày $18$ giờ $ \times \,5 \, = 14$ ngày $10$ giờ . Đúng hay sai?

A. Đúng

B. Sai

Câu 6 :

Điền số thích hợp vào ô trống (dạng thu gọn nhất nếu có thể):

$6,35$ phút $ \times \,\,4\,\, = $

phút

Câu 7 :

Một người thợ làm một sản phẩm hết $2$ giờ $25$ phút. Hỏi người đó làm $8$ sản phẩm như thể hết bao nhiêu thời gian?

A. $16$ giờ $25$ phút

B. $17$ giờ $40$ phút

C. $18$ giờ $20$ phút

D. $19$ giờ $20$ phút

Câu 8 :

Tính : $30$ phút $ + \,2$ giờ $15$ phút $ \times \,\,3$

A. $6$ giờ $45$ phút

B. $6$ giờ $15$ phút

C. $7$ giờ $15$ phút

D. $8$ giờ $15$ phút

Câu 9 :

Điền số thích hợp vào ô trống:

$(3$ phút $25$ giây $ + \,\,5$ phút $45$ giây $)\,\, \times \,\,3$ =

phút

giây.

Câu 10 :

Điền dấu ($>;\,<;\, = $) thích hợp vào ô trống:

$13$ ngày $8$ giờ $ \times \,\,3$

$9$ ngày $7$ giờ $ \times \,4$

Câu 11 :

Một vòi nước chảy vào bể từ lúc $8$ giờ $15$ phút đến $9$ giờ $24$ phút thì được $3,5{m^3}$ nước. Hỏi sau bao lâu bể đầy nước, biết rằng thể tích của bể là $14{m^3}$.

A. $1$ giờ $9$ phút

B. $3$ giờ $48$ phút

C. $4$ giờ $36$ phút

D. $16$ giờ $6$ phút

Câu 12 :

Một người thợ may may một cái áo hết $1$ giờ $45$ phút và may một cái quần hết $1$ giờ $20$ phút. Hỏi người thợ đó may $4$ cái áo và $5$ cái quần hết bao nhiêu thời gian? Biết thời gian may $1$ cái áo, $1$ cái quần không thay đổi.

A. $3$ giờ $5$ phút

B. $6$ giờ $40$ phút

C. $7$ giờ

D. $13$ giờ $40$ phút

Câu 13 :

Một đội công nhân chuyển gạo vào $3$ kho. Thời gian chuyển gạo vào kho thứ nhất là $1$ giờ $24$ phút. Biết thời gian chuyển gạo vào kho thứ hai gấp $3$ lần thời gian chuyển gạo vào kho thứ nhất. Thời gian chuyển gạo vào kho thứ ba gấp $2$ lần thời gian chuyển gạo vào kho thứ hai. Tính tổng thời gian chuyển gạo vào $3$ kho.

A. $14$ giờ

B. $13$ giờ $50$ phút

C. $12$ giờ $36$ phút

D. $8$ giờ $24$ phút

Câu 14 :

Một người đạp xe $3$ vòng thành phố, trong khi đạp mỗi vòng người đó nghỉ lại $20$ phút rồi mới đạp vòng tiếp theo. Biết thời gian đạp vòng đầu tiên là từ $5$ giờ $25$ phút đến $7$ giờ $10$ phút. Hỏi nếu không tính thời gian nghỉ người đó đạp xong $3$ vòng thành phố lúc mấy giờ?

A. $9$ giờ $40$ phút

B. $11$ giờ $15$ phút

C. $10$ giờ $55$ phút

D. $10$ giờ $40$ phút

Lời giải và đáp án

Câu 1 :

Điền số thích hợp vào ô trống:

$1,2$ giờ =

phút.

Đáp án

$1,2$ giờ =

phút.

Phương pháp giải :

Muốn đổi từ đơn vị giờ sang đơn vị phút ta lấy số giờ nhân với $60$ phút.

Lời giải chi tiết :

Ta có $1$ giờ = $60$ phút nên $1,2$ giờ $ = 60$ phút $ \times \,\,1,2\, = \,\,72$ phút.

Vậy đáp án đúng điền vào ô trống là $72$.

Câu 2 :

Điền số thích hợp vào ô trống:

$8,4$ thế kỉ =

năm.

Đáp án

$8,4$ thế kỉ =

năm.

Phương pháp giải :

Muốn đổi từ đơn vị thế kỉ sang đơn vị năm ta lấy số thế kỉ nhân với $100$ năm.

Lời giải chi tiết :

Ta có $1$ thế kỉ = $100$ năm nên $8,4$ thế kỉ $ = 100$ năm $ \times \,\,8,4\, = \,\,840$ năm.

Vậy đáp án đúng điền vào ô trống là $840$.

Câu 3 :

Cho phép tính như sau:

Số thích hợp điền vào ô trống theo thứ tự từ trái sang phải lần lượt là:

A. $6;\,\,45$.

B. $6;\,\,15$.

C. $8;\,\,45$.

D. $8;\,\,15$.

Đáp án

A. $6;\,\,45$.

Phương pháp giải :

- Đặt tính thẳng hàng và thực hiện tính như đối với phép nhân các số tự nhiên.

- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.

- Nếu số phút ở kết quả lớn hơn hoặc bằng $60$ thì ta thực hiện chuyển đổi sang đơn vị lớn hơn phút là giờ.

Lời giải chi tiết :

Ta đặt tính và thực hiện tính như sau:

Vậy $2$ giờ $15$ phút $ \times \,\,3\,\, = \,\,6$ giờ $45$ phút.

Đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là $6;\,\,45$.

Câu 4 :

Tính: $4$ năm $5$ tháng $ \times \,5$.

A. $4$ năm $25$ tháng

B. $20$ năm $5$ tháng

C. $22$ năm $1$ tháng

D. $22$ năm $5$ tháng

Đáp án

C. $22$ năm $1$ tháng

Phương pháp giải :

- Đặt tính thẳng hàng và thực hiện tính như đối với phép nhân các số tự nhiên.

- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.

- Nếu số tháng ở kết quả lớn hơn hoặc bằng $12$ thì ta thực hiện chuyển đổi sang đơn vị lớn hơn tháng là năm.

Lời giải chi tiết :

Ta đặt tính và thực hiện tính như sau:

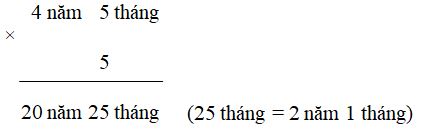
Vậy: $4$ năm $5$ tháng $ \times \,\,5$ $ = \,\,22$ năm $1$ tháng.

Câu 5 :

$2$ ngày $18$ giờ $ \times \,5 \, = 14$ ngày $10$ giờ . Đúng hay sai?

A. Đúng

B. Sai

Đáp án

A. Đúng

B. Sai

Phương pháp giải :

- Đặt tính thẳng hàng và thực hiện tính như đối với phép nhân các số tự nhiên.

- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.

- Nếu số giờ ở kết quả lớn hơn hoặc bằng $24$ thì ta thực hiện chuyển đổi sang đơn vị lớn hơn giờ là ngày.

Lời giải chi tiết :

Ta đặt tính và thực hiện tính như sau:

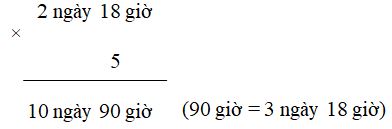
Vậy $2$ ngày $18$ giờ $ \times \,5\, = 13$ ngày $18$ giờ.

Phép tính đã cho chưa đúng.

Câu 6 :

Điền số thích hợp vào ô trống (dạng thu gọn nhất nếu có thể):

$6,35$ phút $ \times \,\,4\,\, = $

phút

Đáp án

$6,35$ phút $ \times \,\,4\,\, = $

phút

Phương pháp giải :

- Đặt tính thẳng hàng và thực hiện tính như phép nhân số thập phân với số tự nhiên.

- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.

Lời giải chi tiết :

Đặt tính và thực hiện tính ta có:

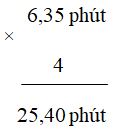
Vậy $6,35$ phút $ \times \,\,4\,\, = \,\,25,4$ phút.

Đáp án đúng điền vào ô trống là $25,4$.

Câu 7 :

Một người thợ làm một sản phẩm hết $2$ giờ $25$ phút. Hỏi người đó làm $8$ sản phẩm như thể hết bao nhiêu thời gian?

A. $16$ giờ $25$ phút

B. $17$ giờ $40$ phút

C. $18$ giờ $20$ phút

D. $19$ giờ $20$ phút

Đáp án

D. $19$ giờ $20$ phút

Phương pháp giải :

Tính thời gian người đó làm $8$ sản phẩm ta lấy thời gian làm một sản phẩm nhân với $8$.

Lời giải chi tiết :

Người đó làm $8$ sản phẩm như thể hết số thời gian là:

$2$ giờ $25$ phút $ \times \,\,8\,\, = \,\,16$ giờ $200$ phút $ = \,\,19$ giờ $20$ phút

Đáp số: $19$ giờ $20$ phút.

Câu 8 :

Tính : $30$ phút $ + \,2$ giờ $15$ phút $ \times \,\,3$

A. $6$ giờ $45$ phút

B. $6$ giờ $15$ phút

C. $7$ giờ $15$ phút

D. $8$ giờ $15$ phút

Đáp án

C. $7$ giờ $15$ phút

Phương pháp giải :

- Thực hiện tính giá trị biểu thức như đối với các số tự nhiên, trong biểu thức có phép cộng và phép nhân thì ta tính phép nhân trước, tính phép cộng sau.

- Sau mỗi kết quả ta phải ghi số đo tương ứng

- Trong khi thực hiện tính giá trị biểu thức, nếu số giây lớn hơn hoặc bằng $60$ thì ta thực hiện chuyển đổi sang đơn vị lớn hơn của giây là phút.

Lời giải chi tiết :

Ta có:

$30$ phút $ + \,\,2$ giờ $15$ phút $ \times \,\,3$

$ = \,\,30$ phút $ + \,\,6$ giờ $45$ phút

$ = \,\,6$ giờ $75$ phút

$ = \,\,7$ giờ $15$ phút

Câu 9 :

Điền số thích hợp vào ô trống:

$(3$ phút $25$ giây $ + \,\,5$ phút $45$ giây $)\,\, \times \,\,3$ =

phút

giây.

Đáp án

$(3$ phút $25$ giây $ + \,\,5$ phút $45$ giây $)\,\, \times \,\,3$ =

phút

giây.

Phương pháp giải :

- Thực hiện tính giá trị biểu thức như đối với các số tự nhiên, tính lần lượt trong ngoặc trước ngoài ngoặc sau

- Sau mỗi kết quả ta phải ghi số đo tương ứng.

- Trong khi thực hiện tính giá trị biểu thức, nếu số giây lớn hơn hoặc bằng $60$ thì ta thực hiện chuyển đổi sang đơn vị lớn hơn của giây là phút.

Lời giải chi tiết :

Ta có:

$(3$ phút $25$ giây $ + \,\,5$ phút $45$ giây $)\,\, \times \,\,3$

$ = \,\,\,8$ phút $70$ giây $\,\, \times \,\,3$

$ = \,\,\,9$ phút $10$ giây $\,\, \times \,\,3$ (vì $70$ giây $ = \,\,1$ phút $10$ giây)

$ = \,\,\,27$ phút $30$ giây

Vậy đáp án cần điền vào ô trống lần lượt từ trái sang phải là $27;\,\,30$.

Câu 10 :

Điền dấu ($>;\,<;\, = $) thích hợp vào ô trống:

$13$ ngày $8$ giờ $ \times \,\,3$

$9$ ngày $7$ giờ $ \times \,4$

Đáp án

$13$ ngày $8$ giờ $ \times \,\,3$

$9$ ngày $7$ giờ $ \times \,4$

Phương pháp giải :

Tính giá trị hai vế rồi so sánh kết quả với nhau.

Lời giải chi tiết :

Ta có:

+) $13$ ngày $8$ giờ $ \times \,\,3\,\, = \,\,39$ ngày $24$ giờ $ = \,40$ ngày (vì $24$ giờ $ = \,1$ ngày).

+) $9$ ngày $7$ giờ $ \times \,\,4\,\, = \,\,36$ ngày $28$ giờ $ = \,37$ ngày $4$ giờ (vì $28$ giờ $ = \,1$ ngày $4$ giờ).

Mà $40$ ngày $ > \,37$ ngày $4$ giờ.

Vậy $13$ ngày $8$ giờ $ \times \,\,3\,\,> \,\,9$ ngày $7$ giờ $ \times \,4$.

Câu 11 :

A. $1$ giờ $9$ phút

B. $3$ giờ $48$ phút

C. $4$ giờ $36$ phút

D. $16$ giờ $6$ phút

Đáp án

C. $4$ giờ $36$ phút

Phương pháp giải :

Đây là dạng bài toán về tỉ lệ luận. Ta có thể giải bài toán này bằng cách tìm “tỉ số”:

- Tìm thời gian để vòi chảy vào bể được $3,5{m^3}$ nước ta tính $9$ giờ $24$ phút $ - \,8$ giờ $15$ phút.

- Tìm tỉ số giữa $14{m^3}$ và $3,5{m^3}$ ta có $14:3,5 = 4$.

- Tìm thời gian để bể đầy nước ta lấy thời gian để vòi chảy vào bể được $3,5{m^3}$ nước nhân với $4$.

Lời giải chi tiết :

Thời gian để vòi chảy vào bể được $3,5{m^3}$ nước là:

$9$ giờ $24$ phút $ - \,\,8$ giờ $15$ phút $ = \,\,1$ giờ $9$ phút

$14{m^3}$ gấp $3,5{m^3}$ số lần là:

$14:3,5 = 4$ (lần)

Bể đầy nước sau số thời gian là:

$1$ giờ $9$ phút $ \times \,\,4\,\, = \,\,4$ giờ $36$ phút

Đáp số: $4$ giờ $36$ phút

Câu 12 :

A. $3$ giờ $5$ phút

B. $6$ giờ $40$ phút

C. $7$ giờ

D. $13$ giờ $40$ phút

Đáp án

D. $13$ giờ $40$ phút

Phương pháp giải :

- Tính thời gian để may $4$ cái áo $=$ thời gian may $1$ cái áo $ \times \,4$.

- Tính thời gian để may $5$ cái quần $=$ thời gian may $1$ cái quần $ \times \,5$.

- Tìm thời gian may $4$ cái áo và $5$ cái quần $=$ thời gian để may $4$ cái áo $+$ thời gian để may $5$ cái quần.

Lời giải chi tiết :

Thời gian để may $4$ cái áo là:

$1$ giờ $45$ phút $ \times \,\,4\,\, = \,\,4$ giờ $180$ phút $ = \,\,7$ giờ

Thời gian để may $5$ cái quần là:

$1$ giờ $20$ phút $ \times \,\,5\,\, = \,\,5$ giờ $100$ phút $ = \,\,6$ giờ $40$ phút

Người thợ đó may $4$ cái áo và $5$ cái quần hết số thời gian là:

$7$ giờ $ + \,\,6$ giờ $40$ phút $ = \,\,13$ giờ $40$ phút

Đáp số: $13$ giờ $40$ phút.

Câu 13 :

A. $14$ giờ

B. $13$ giờ $50$ phút

C. $12$ giờ $36$ phút

D. $8$ giờ $24$ phút

Đáp án

A. $14$ giờ

Phương pháp giải :

- Tìm thời gian chuyển gạo vào kho thứ hai = thời gian chuyển gạo vào kho thứ nhất $ \times \,\,3$.

- Tìm thời gian chuyển gạo vào kho thứ ba = thời gian chuyển gạo vào kho thứ hai $ \times \,\,2$.

- Tìm tổng thời gian chuyển gạo vào cả 3 kho

Lưu ý: Nếu số phút lớn hơn hoặc bằng $60$ thì ta thực hiện chuyển đổi sang đơn vị lớn hơn của phút là giờ.

Lời giải chi tiết :

Thời gian chuyển gạo vào kho thứ hai là:

$1$ giờ $24$ phút $ \times \,3\, = \,3$ giờ $72$ phút $ = \,4$ giờ $12$ phút

Thời gian chuyển gạo vào kho thứ ba là:

$4$ giờ $12$ phút $ \times \,2\, = \,8$ giờ $24$ phút

Tổng thời gian chuyển gạo vào cả $3$ kho là:

$1$ giờ $24$ phút $ + \,4$ giờ $12$ phút $ + \,8$ giờ $24$ phút $ = \,13$ giờ $60$ phút $ = \,14$ giờ

Đáp số: $14$ giờ.

Câu 14 :

A. $9$ giờ $40$ phút

B. $11$ giờ $15$ phút

C. $10$ giờ $55$ phút

D. $10$ giờ $40$ phút

Đáp án

A. $9$ giờ $40$ phút

Phương pháp giải :

- Tìm thời gian người đó đi hết $1$ vòng thành phố tính cả thời gian nghỉ = $7$ giờ $10$ phút $ - \,5$ giờ $25$ phút.

- Tìm thời gian người đó đi hết $1$ vòng thành phố không tính thời gian nghỉ ta lấy thời gian người đó đi hết $1$ vòng thành phố tính cả thời gian nghỉ trừ đi thời gian nghỉ.

- Tìm thời gian người đó đi hết $3$ vòng thành phố nếu không tính thời gian nghỉ ta lấy thời gian đi hết $1$ vòng thành phố không tính thời gian nghỉ nhân với $3$.

- Tìm thời gian lúc người đó đạp xe xong $3$ vòng thành phố không tính thời gian nghỉ ta lấy thời gian lúc người đó bắt đầu xuất phát cộng với thời gian người đó đi hết $3$ vòng thành phố nếu không tính thời gian nghỉ.

Lưu ý: Nếu số phút lớn hơn hoặc bằng $60$ thì ta thực hiện chuyển đổi sang đơn vị lớn hơn của phút là giờ.

Lời giải chi tiết :

Thời gian người đó đi hết $1$ vòng thành phố tính cả thời gian nghỉ là:

$7$ giờ $10$ phút $ - \,5$ giờ $25$ phút $ = \,1$ giờ $45$ phút

Thời gian người đó đi hết $1$ vòng thành phố không tính thời gian nghỉ là:

$1$ giờ $45$ phút $ - \,20$ phút $ = \,1$ giờ $25$ phút

Thời gian người đó đi hết $3$ vòng thành phố không tính thời gian nghỉ là:

$1$ giờ $25$ phút $ \times \,3\, = \,3$ giờ $75$ phút $\, = \,4$ giờ $15$ phút

Nếu không tính thời gian nghỉ người đó đạp xong $3$ vòng thành phố lúc:

$5$ giờ $25$ phút $ + \,4$ giờ $15$ phút $\, = \,9$ giờ $40$ phút

Đáp số: $9$ giờ $40$ phút.

Trắc nghiệm: Chia số đo thời gian cho một số Toán 5

Luyện tập và củng cố kiến thức Chia số đo thời gian cho một số Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Luyện tập về số đo thời gian và các phép tính với số đo thời gian Toán 5

Luyện tập và củng cố kiến thức Luyện tập về số đo thời gian và các phép tính với số đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Vận tốc Toán 5

Luyện tập và củng cố kiến thức Vận tốc Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Quãng đường Toán 5

Luyện tập và củng cố kiến thức Quãng đường Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Thời gian Toán 5

Luyện tập và củng cố kiến thức Thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Hai vật chuyển động ngược chiều Toán 5

Luyện tập và củng cố kiến thức Hai vật chuyển động ngược chiều Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Hai vật chuyển động cùng chiều Toán 5

Luyện tập và củng cố kiến thức Hai vật chuyển động cùng chiều Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Chuyển động trên dòng nước Toán 5

Luyện tập và củng cố kiến thức Chuyển động trên dòng nước Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Trừ số đo thời gian Toán 5

Luyện tập và củng cố kiến thức Trừ số đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Cộng số đo thời gian Toán 5

Luyện tập và củng cố kiến thức Cộng số đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm: Bảng đơn vị đo thời gian Toán 5

Luyện tập và củng cố kiến thức Bảng đơn vị đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Bài giải mới nhất

Trắc nghiệm: Nhân số đo thời gian với một số Toán 5

Báo lỗi góp ý