-
Chương 1. Ôn tâp và bổ sung về phân số. Giải toán liên quan đến tỉ lệ. Bảng đơn vị đo diện tích
- Ôn tập khái niệm về phân số. Tính chất cơ bản của phân số
- Ôn tập: So sánh hai phân số
- Ôn tập: So sánh hai phân số (tiếp)
- Phân số thập phân
- Ôn tập: Phép cộng và phép trừ hai phân số
- Ôn tập: Phép nhân và phép chia hai phân số
- Hỗn số
- Hỗn số (tiếp theo)
- Luyện tập chung về phân số và hỗn số
- Ôn tập về giải toán
- Ôn tập và bổ sung về giải toán
- Ôn tập: Bảng đơn vị đo độ dài
- Ôn tập: Bảng đơn vị đo khối lượng
- Đề-ca-mét vuông. Héc-tô-mét vuông. Héc-ta
- Mi-li-mét vuông. Bảng đơn vị đo diện tích
- Ôn tập chương 1
-
Chương 2. Số thập phân. Các phép tính với số thập phân
- Khái niệm số thập phân
- Hàng của số thập phân. Đọc, viết số thập phân
- Số thập phân bằng nhau. So sánh hai số thập phân
- Viết các số đo độ dài dưới dạng số thập phân
- Viết các số đo khối lượng dưới dạng số thập phân
- Viết các số đo diện tích dưới dạng số thập phân
- Luyện tập về số thập phân
- Phép cộng số thập phân. Tổng nhiều số thập phân
- Phép trừ hai số thập phân
- Luyện tập về phép cộng và phép trừ số thập phân
- Nhân một số thập phân với một số tự nhiên
- Nhân một số thập phân với 10, 100, 1000, …
- Nhân một số thập phân với một số thập phân
- Luyện tập về phép nhân số thập phân
- Chia một số thập phân cho một số tự nhiên
- Chia một số thập phân cho 10, 100, 1000, …
- Chia một số tự nhiên cho một số tự nhiên mà thương tìm được là một số thập phân
- Chia một số tự nhiên cho một số thập phân
- Chia một số thập phân cho một số thập phân
- Luyện tập về phép chia số thập phân
- Tỉ số phần trăm. Các phép tính với tỉ số phần trăm
- Giải toán về tỉ số phần trăm: Tìm tỉ số phần trăm của hai số
- Giải toán về tỉ số phần trăm: Tìm giá trị phần trăm của một số
- Giải toán về tỉ số phần trăm: Tìm một số khi biết giá trị phần trăm của số đó
- Giải toán về tỉ số phần trăm: Tỉ số phần trăm liên quan đến mua bán
- Ôn tập chương 2
-
Chương 3. Hình học
- Hình tam giác. Diện tích hình tam giác
- Hình thang. Diện tích hình thang
- Hình tròn. Đường tròn. Chu vi hình tròn
- Diện tích hình tròn
- Luyện tập về diện tích các hình
- Hình hộp chữ nhật. Hình lập phương
- Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật
- Diện tích xung quanh và diện tích toàn phần của hình lập phương
- Thể tích của một hình. Xăng-ti-mét khối. Đề-xi-mét khối. Mét khối
- Thể tích hình hộp chữ nhật
- Thể tích hình lập phương
- Ôn tập chương 3
-
Chương 4. Số đo thời gian. Toán chuyển động đều
- Bảng đơn vị đo thời gian
- Cộng số đo thời gian
- Trừ số đo thời gian
- Nhân số đo thời gian với một số
- Chia số đo thời gian cho một số
- Luyện tập về số đo thời gian và các phép tính với số đo thời gian
- Vận tốc
- Quãng đường
- Thời gian
- Hai vật chuyển động ngược chiều
- Hai vật chuyển động cùng chiều
- Chuyển động trên dòng nước
-
Chương 5. Ôn tập
- Ôn tập về số tự nhiên
- Ôn tập về phân số
- Ôn tập về số thập phân
- Ôn tập về đo độ dài và đo khối lượng
- Ôn tập về đo diện tích và đo thể tích
- Ôn tập về số đo thời gian
- Ôn tập về phép cộng
- Ôn tập về phép trừ
- Ôn tập về phép nhân
- Ôn tập về phép chia
- Ôn tập các phép tính với số đo thời gian
- Ôn tập về hình học: Tính chu vi, diện tích một số hình
- Ôn tập về hình học: Tính diện tích, thể tích một số hình
Trắc nghiệm: Ôn tập về hình học: Tính chu vi, diện tích một số hình Toán 5
Đề bài
A. Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\).
B. Muốn tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\).
C. Muốn tính diện tích của hình tròn ta lấy bán kính nhân với bán kính rồi nhân với số \(3,14\).
D. Cả A, B, C đều đúng.
A. Muốn tính chu vi hình vuông ta lấy độ dài một cạnh nhân với \(4\).
B. Muốn tính chu vi hình chữ nhật ta lấy tổng độ dài chiều dài và chiều rộng nhân với \(2\).
C. Muốn tính chu vi hình tròn ta lấy đường kính nhân với số \(3,14\).
D. Tất cả các đáp án trên đều đúng.
Điền số thích hợp vào ô trống:
Một hình tam giác có độ dài đáy là \(36cm\), chiều cao tương ứng bằng \(\dfrac{3}{4}\) độ dài đáy.
Vậy diện tích tam giác đó là
\(cm^2\).
Điền số thích hợp vào ô trống:
Một hình thang có đáy bé bằng $24cm$, đáy bé bằng \(\dfrac{4}{7}\) đáy lớn, chiều cao bằng \(\dfrac{1}{2}\) đáy lớn.
Vậy diện tích của hình thang đó là
\(cm^2\).
Một hình tròn có diện tích là \(200,96d{m^2}\). Tính chu vi hình tròn đó.
A. \(25,12dm\)
B. \(50,24dm\)
C. \(100,48dm\)
D. \(12861,44dm\)
Điền số thích hợp vào ô trống:
Một sân gạch hình vuông có chu vi \(52m\). Vậy diện tích sân gạch đó là
\({m^2}\).
Một hình tam giác có diện tích bằng diện tích hình bình hành có độ dài đáy là \(36cm\), chiều cao tương ứng là \(15cm\). Tính độ dài đáy của hình tam giác, biết chiều cao tương ứng với đáy của hình tam giác bằng \(\dfrac{2}{3}\) độ dài đáy của hình bình hành đó.
A. \(25cm\)
B. \(11,25cm\)
C. \(22,5cm\)
D. \(45cm\)
Một thửa ruộng hình thang có đáy lớn \(160m\), đáy bé bằng \(\dfrac{3}{5}\) đáy lớn, chiều cao bằng trung bình cộng độ dài hai đáy. Bác Khánh trồng lúa trên thửa ruộng đó, trung bình cứ \(100{m^2}\) thì thu được \(65kg\) thóc. Hỏi bác Khánh thu hoạch được bao nhiêu tấn thóc trên thửa ruộng đó?
A. \(10,6496\) tấn
B. \(106,496\) tấn
C. \(1064,96\) tấn
D. \(10649,6\) tấn
Điền số thích hợp vào ô trống:
Một mảnh đất được vẽ trên bản đồ tỉ lệ \(1:1000\) với kích thước như hình vẽ:
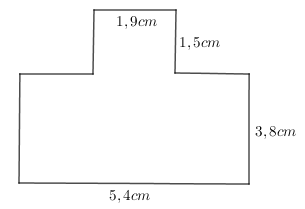
Vậy diện tích mảnh đất đó trong thực tế là
\(m^2\).
Điền số thích hợp vào ô trống (dạng thu gọn nhất):
Một hình thoi độ dài hai đường chéo là \(48cm\) và \(27cm\). Một hình chữ nhật có chiều rộng là \(36cm\) và có diện tích gấp \(3\) lần diện tích hình thoi.
Vậy chu vi hình chữ nhật đó là
\(m\).
Một miếng đất hình thang có diện tích là $864{m^2}$, đáy lớn hơn đáy bé 12m. Người ta mở rộng miếng đất bằng cách tăng đáy lớn thêm $5m$ thì được miếng đất hình thang mới có diện tích bằng $924{m^2}$. Tìm độ dài mỗi đáy của miếng đất hình thang lúc chưa mở rộng.
A. Đáy lớn: \(24m\); đáy bé \(12m\)
B. Đáy lớn: \(42m\); đáy bé \(30m\)
C. Đáy lớn: \(78m\); đáy bé \(66m\)
D. Đáy lớn: \(50m\); đáy bé \(38m\)
Điền số thích hợp vào ô trống:
Cho hình vẽ như sau:
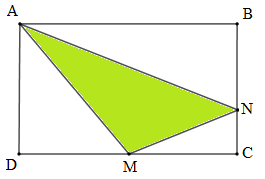
Biết hình chữ nhật $ABCD$ có diện tích bằng \(96c{m^2};{\rm{ }}MC{\rm{ }} = {\rm{ }}MD;\,\,BN = \dfrac{2}{3}BC\) (như hình vẽ).
Diện tích tam giác $AMN$ là
\(cm^2\).
Lời giải và đáp án
A. Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\).
B. Muốn tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\).
C. Muốn tính diện tích của hình tròn ta lấy bán kính nhân với bán kính rồi nhân với số \(3,14\).
D. Cả A, B, C đều đúng.
D. Cả A, B, C đều đúng.
Dựa vào quy tắc tính diện tích các hình tam giác, hình thang, hình tròn.
- Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2.\)
- Muốn tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2.\)
- Muốn tính diện tích của hình tròn ta lấy bán kính nhân với bán kính rồi nhân với số \(3,14\).
Vậy cả A, B, C đều đúng.
A. Muốn tính chu vi hình vuông ta lấy độ dài một cạnh nhân với \(4\).
B. Muốn tính chu vi hình chữ nhật ta lấy tổng độ dài chiều dài và chiều rộng nhân với \(2\).
C. Muốn tính chu vi hình tròn ta lấy đường kính nhân với số \(3,14\).
D. Tất cả các đáp án trên đều đúng.
D. Tất cả các đáp án trên đều đúng.
Dựa vào quy tắc tính chu vi các hình vuông, hình chữ nhật và hình tròn.
- Muốn tính chu vi hình vuông ta lấy độ dài một cạnh nhân với \(4\).
- Muốn tính chu vi hình chữ nhật ta lấy tổng độ dài chiều dài và chiều rộng nhân với \(2\).
- Muốn tính chu vi hình tròn ta lấy đường kính nhân với số \(3,14\).
Vậy tất cả các đáp án đã cho đều đúng.
Điền số thích hợp vào ô trống:
Một hình tam giác có độ dài đáy là \(36cm\), chiều cao tương ứng bằng \(\dfrac{3}{4}\) độ dài đáy.
Vậy diện tích tam giác đó là
\(cm^2\).
Một hình tam giác có độ dài đáy là \(36cm\), chiều cao tương ứng bằng \(\dfrac{3}{4}\) độ dài đáy.
Vậy diện tích tam giác đó là
\(cm^2\).
- Tính chiều cao tương ứng với độ dài đáy ta lấy độ dài đáy chia cho \(4\) rồi nhân với \(3\) hoặc lấy độ dài đáy nhân với \(\dfrac{3}{4}\) .
- Tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\).
Chiều cao tương ứng với độ dài đáy là:
\(36 \times \dfrac{3}{4} = 27\;(cm)\)
Diện tích hình tam giác đó là:
\(36 \times 27:2 = 486\;(c{m^2})\)
Đáp số: \(486c{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(486\).
Điền số thích hợp vào ô trống:
Một hình thang có đáy bé bằng $24cm$, đáy bé bằng \(\dfrac{4}{7}\) đáy lớn, chiều cao bằng \(\dfrac{1}{2}\) đáy lớn.
Vậy diện tích của hình thang đó là
\(cm^2\).
Một hình thang có đáy bé bằng $24cm$, đáy bé bằng \(\dfrac{4}{7}\) đáy lớn, chiều cao bằng \(\dfrac{1}{2}\) đáy lớn.
Vậy diện tích của hình thang đó là
\(cm^2\).
- Tìm độ dài đáy lớn ta lấy độ dài đáy bé chia cho \(4\) rồi nhân với \(7\).
- Tính chiều cao ta lấy độ dài đáy lớn chia cho \(2\) rồi nhân \(1\) hoặc lấy độ dài đáy lớn nhân với \(\dfrac{1}{2}\).
- Tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\).
Độ dài đáy lớn là:
$24:4 \times 7 = 42\;(cm)$
Chiều cao của hình thang đó là:
$42:2 \times 1 = 21\,(cm)$
Diện tích hình thang đó là:
$(42 + 24) \times 21:2 = 693\;(c{m^2})$
Đáp số: \(693c{m^2}\).
Một hình tròn có diện tích là \(200,96d{m^2}\). Tính chu vi hình tròn đó.
A. \(25,12dm\)
B. \(50,24dm\)
C. \(100,48dm\)
D. \(12861,44dm\)
B. \(50,24dm\)
- Từ công thức tính diện tích \(S = r \times r \times 3,14\), ta có thể tính tích của bán kính với bán kính theo công thức: \(r \times r = S:3,14\), sau đó lập luận để tìm ra bán kính \(r\).
- Tính chu vi hình tròn theo công thức \(C = r \times 2 \times 3,14\).
Tích của bán kính và bán kính là:
\(200,96:3,14 = 64\;(d{m^2})\)
Vì \(8 \times 8 = 64\) nên bán kính của mặt bán đó là \(8dm\).
Chu vi mặt bàn đó là:
\(S = 8 \times 2 \times 3,14 = 50,24\;(dm)\).
Đáp số: \(50,24dm\).
Điền số thích hợp vào ô trống:
Một sân gạch hình vuông có chu vi \(52m\). Vậy diện tích sân gạch đó là
\({m^2}\).
Một sân gạch hình vuông có chu vi \(52m\). Vậy diện tích sân gạch đó là
\({m^2}\).
- Tính độ dài cạnh của sân đó ta lấy chu vi chia cho \(4\).
- Tính diện tích sân ta lấy độ dài cạnh nhân với độ dài cạnh
Độ dài cạnh của sân đó là:
\(52:4 = 13\;(m)\)
Diện tích sân gạch đó là:
\(13 \times 13 = 169\;({m^2})\)
Đáp số: \(169{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(169\).
Một hình tam giác có diện tích bằng diện tích hình bình hành có độ dài đáy là \(36cm\), chiều cao tương ứng là \(15cm\). Tính độ dài đáy của hình tam giác, biết chiều cao tương ứng với đáy của hình tam giác bằng \(\dfrac{2}{3}\) độ dài đáy của hình bình hành đó.
A. \(25cm\)
B. \(11,25cm\)
C. \(22,5cm\)
D. \(45cm\)
D. \(45cm\)
- Tính diện tích bình hành ta lấy độ dài đáy nhân với chiều cao tương ứng.
- Vì hình tam giác có diện tích bằng diện tích hình bình hành nên ta tìm được diện tích hình tam giác.
- Tính chiều cao của hình tam giác ta lấy độ dài đáy của hình bình hành nhân với \(\dfrac{2}{3}\) hoặc lấy độ dài đáy của hình bình hành chia cho \(3\) và nhân với \(2\).
- Tính độ dài đáy của hình tam giác ta lấy diện tích tam giác nhân với \(2\) rồi chia cho chiều cao.
Diện tích hình bình hành là:
\(36 \times 15 = 540\;(c{m^2})\)
Vì hình tam giác có diện tích bằng diện tích hình bình hành nên diện tích hình tam giác là \(540c{m^2}\).
Chiều cao của hình tam giác là:
\(36:3 \times 2 = 24\;(cm)\)
Độ dài đáy của hình tam giác là:
\(540 \times 2:24 = 45\;(cm)\)
Đáp số: \(45cm\).
Một thửa ruộng hình thang có đáy lớn \(160m\), đáy bé bằng \(\dfrac{3}{5}\) đáy lớn, chiều cao bằng trung bình cộng độ dài hai đáy. Bác Khánh trồng lúa trên thửa ruộng đó, trung bình cứ \(100{m^2}\) thì thu được \(65kg\) thóc. Hỏi bác Khánh thu hoạch được bao nhiêu tấn thóc trên thửa ruộng đó?
A. \(10,6496\) tấn
B. \(106,496\) tấn
C. \(1064,96\) tấn
D. \(10649,6\) tấn
A. \(10,6496\) tấn
- Tính độ dài đáy bé ta lấy độ dài đáy lớn nhân với \(\dfrac{3}{5}\) hoặc lấy độ dài đáy lớn chia cho \(5\) và nhân với \(3\).
- Tính chiều cao ta lấy tổng độ dài hai đáy chia cho \(2\).
- Tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho \(2\).
- Tìm số thóc thu được theo bài toán tỉ lệ thuận: tìm tỉ số giữa diện tích và \(100{m^2}\), diện tích gấp \(100{m^2}\) bao nhiêu lần thì số thóc thu được cũng gấp \(65kg\) bấy nhiêu lần.
- Đổi số đo khối lượng vừa tìm được sang đơn vị đo là tấn.
Độ dài đáy bé của thửa ruộng đó là:
\(160 \times \dfrac{3}{5} = 96\;(m)\)
Chiều cao của thửa ruộng đó là:
\((160 + 96):2 = 128\;(m)\)
Diện tích thửa ruộng đó là:
\((160 + 96) \times 128:2 = 16384\;({m^2})\)
Trên thửa ruộng đó, bác Khánh thu được số ki-lô-gam thóc là:
\((16384:100) \times 65 = 10649,6\;(kg)\)
\(10649,6kg\, = \,10,6496\) tấn
Đáp số: \(10,6496\) tấn.
Điền số thích hợp vào ô trống:
Một mảnh đất được vẽ trên bản đồ tỉ lệ \(1:1000\) với kích thước như hình vẽ:
Vậy diện tích mảnh đất đó trong thực tế là
\(m^2\).
Một mảnh đất được vẽ trên bản đồ tỉ lệ \(1:1000\) với kích thước như hình vẽ:
Vậy diện tích mảnh đất đó trong thực tế là
\(m^2\).
- Chia mảnh đất đã cho thành các hình chữ nhật nhỏ.
- Tính chiều dài và chiều rộng thực tế của các các mảnh đất đó theo công thức:
Độ dài thực tế \( = \) độ dài trên bản đồ \( \times \,\,1000\) (do bản đồ có tỉ lệ \(1:1000\))
- Đổi các số đo độ dài sang đơn vị mét.
- Tính diện tích thực tế của các mảnh đất ta lấy chiều dài thực tế nhân với chiều rộng thực tế.
- Diện tích mảnh đất ban đầu bằng tổng diện tích các mảnh đất đã được chia.
Ta chia mảnh đất ban đầu thành hai hình như hình vẽ:
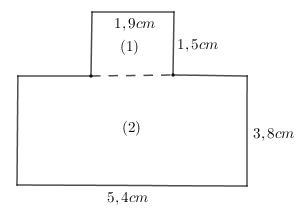
Chiều dài thực tế của mảnh đất \(1\) là:
\(1,9 \times 1000 = 1900\;(cm) = 19\;(m)\)
Chiều rộng thực tế của mảnh đất \(1\) là:
\(1,5 \times 1000 = 1500\;(cm) = 15\;(m)\)
Diện tích thực tế của mảnh đất \(1\) là:
\(19 \times 15 = 285\;({m^2})\)
Chiều dài thực tế của mảnh đất \(2\) là:
\(5,4 \times 1000 = 5400\;(cm) = 54\;(m)\)
Chiều rộng thực tế của mảnh đất \(2\) là:
\(3,8 \times 1000 = 3800\;(cm) = 38\;(m)\)
Diện tích thực tế của mảnh đất \(2\) là:
\(54 \times 38 = 2052\;({m^2})\)
Diện tích thực tế của mảnh đất ban đầu là:
\(285 + 2052 = 2337\;({m^2})\)
Đáp số: \(2337{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(2337\).
Điền số thích hợp vào ô trống (dạng thu gọn nhất):
Một hình thoi độ dài hai đường chéo là \(48cm\) và \(27cm\). Một hình chữ nhật có chiều rộng là \(36cm\) và có diện tích gấp \(3\) lần diện tích hình thoi.
Vậy chu vi hình chữ nhật đó là
\(m\).
Một hình thoi độ dài hai đường chéo là \(48cm\) và \(27cm\). Một hình chữ nhật có chiều rộng là \(36cm\) và có diện tích gấp \(3\) lần diện tích hình thoi.
Vậy chu vi hình chữ nhật đó là
\(m\).
- Tính diện tích hình thoi ta lấy tích độ dài hai đường chéo chia cho \(2\).
- Tính diện tích hình chữ nhật ta lấy diện tích hình thoi nhân với \(3\).
- Tính chiều dài hình chữ nhật ta lấy diện tích hình chữ nhật chia cho chiều rộng.
- Tính chu vi hình chữ nhật ta tính tổng của chiều dài và chiều rộng rồi nhân với \(2\).
- Đổi số đo độ dài vừa tìm được sang đơn vị đo là mét.
Diện tích hình thoi là:
\(48 \times 27:2 = 648\;(c{m^2})\)
Diện tích hình chữ nhật là:
\(648 \times 3 = 1944\;(c{m^2})\)
Chiều dài hình chữ nhật là:
\(1944:36 = 54\;(cm)\)
Chu vi hình chữ nhật là:
\((54 + 36) \times 2 = 180\;(cm)\)
Đổi \(180cm = 1,8m\)
Đáp số: \(1,8m\).
Vậy đáp án đúng điền vào ô trống là \(1,8\).
Một miếng đất hình thang có diện tích là $864{m^2}$, đáy lớn hơn đáy bé 12m. Người ta mở rộng miếng đất bằng cách tăng đáy lớn thêm $5m$ thì được miếng đất hình thang mới có diện tích bằng $924{m^2}$. Tìm độ dài mỗi đáy của miếng đất hình thang lúc chưa mở rộng.
A. Đáy lớn: \(24m\); đáy bé \(12m\)
B. Đáy lớn: \(42m\); đáy bé \(30m\)
C. Đáy lớn: \(78m\); đáy bé \(66m\)
D. Đáy lớn: \(50m\); đáy bé \(38m\)
B. Đáy lớn: \(42m\); đáy bé \(30m\)
- Tính diện tích phần đất tăng thêm.
Diện tích phần đất tăng thêm chính là diện tích hình tam giác có độ dài đáy là \(5m\) và chiều cao là chiều cao của hình thang.
- Tính chiều cao của hình thang ta lấy diện tích phần đất tăng thêm nhân với \(2\) rồi chia cho độ dài đáy \(5m\).
- Tính tổng độ dài hai đáy của hình thang ta lấy diện tích hình thang nhân với \(2\) rồi chia cho chiều cao.
- Giải bài toán tìm hai số khi biết tổng và hiệu để tìm độ dài mỗi đáy theo công thức:
Số lớn = (tổng + hiệu) \(:\,\,2\) ; Số bé = (tổng – hiệu) \(:\,\,2\)
Ta có hình vẽ như sau:
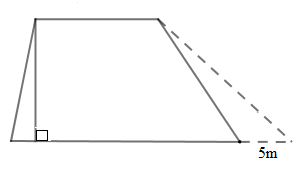
Sau khi mở rộng, diện tích miếng đất tăng thêm là:
$924 - 864 = 60\;({m^2})$
Diện tích phần đất tăng thêm chính là diện tích hình tam giác có độ dài đáy là \(5m\) và chiều cao là chiều cao của hình thang.
Chiều cao của miếng đất hình thang là:
\(60 \times 2:5 = 24\;(m)\)
Tổng độ dài hai đáy của hình thang là:
\(864 \times 2:24 = 72\;(m)\)
Độ dài đáy lớn của miếng đất đó là:
\((72 + 12):2 = 42\;(m)\)
Độ dài đáy bé của miếng đất đó là:
\(72 - 42 = 30\;(m)\)
Đáp số: đáy lớn: \(42m\); đáy bé: \(30m\).
Điền số thích hợp vào ô trống:
Cho hình vẽ như sau:
Biết hình chữ nhật $ABCD$ có diện tích bằng \(96c{m^2};{\rm{ }}MC{\rm{ }} = {\rm{ }}MD;\,\,BN = \dfrac{2}{3}BC\) (như hình vẽ).
Diện tích tam giác $AMN$ là
\(cm^2\).
Cho hình vẽ như sau:
Biết hình chữ nhật $ABCD$ có diện tích bằng \(96c{m^2};{\rm{ }}MC{\rm{ }} = {\rm{ }}MD;\,\,BN = \dfrac{2}{3}BC\) (như hình vẽ).
Diện tích tam giác $AMN$ là
\(cm^2\).
Diện tích tam giác $AMN$ bằng diện tích hình chữ nhật $ABCD$ trừ đi tổng diện tích ba tam giác vuông \(ABN,MNC,ADM\).
- Tính diện tích tam giác \(ADM\):
\({S_{ADM}} = \dfrac{1}{2} \times AD \times DM = \dfrac{1}{2} \times AD \times \dfrac{{DC}}{2} = \dfrac{1}{4} \times AD \times DC\)
Từ đó suy ra diện tích tam giác \(ADM\) bằng \(\dfrac{1}{4}\) diện tích hình chữ nhật $ABCD$.
- Tương tự ta tính được diện tích hai tam giác \(ABN,\,MNC\).
Theo đề bài:
\(\begin{array}{l}MC{\rm{ }} = {\rm{ }}MD \Rightarrow MC = MD = \dfrac{1}{2}DC\\BN = \dfrac{2}{3}BC \Rightarrow NC = \dfrac{1}{3}BC\end{array}\)
Ta có:
+) \({S_{ADM}} = \dfrac{1}{2} \times AD \times DM = \dfrac{1}{2} \times AD \times \dfrac{{DC}}{2} = \dfrac{1}{4} \times AD \times DC\)
Suy ra diện tích tam giác \(ADM\) bằng \(\dfrac{1}{4}\) diện tích hình chữ nhật $ABCD$.
Diện tích tam giác \(ADM\) là:
\(96:4 = 24\;(c{m^2})\)
+) \({S_{ABN}} = \dfrac{1}{2} \times AB \times BN = \dfrac{1}{2} \times AB \times \dfrac{2}{3}BC = \dfrac{1}{3} \times AB \times BC\)
Suy ra diện tích tam giác \(ABN\) bằng \(\dfrac{1}{3}\) diện tích hình chữ nhật $ABCD$.
Diện tích tam giác \(ABN\) là:
\(96:3 = 32\;(c{m^2})\)
+) \({S_{MNC}} = \dfrac{1}{2} \times MC \times NC = \dfrac{1}{2} \times \dfrac{1}{2}DC \times \dfrac{1}{3}BC = \dfrac{1}{{12}} \times DC \times BC\)
Suy ra diện tích tam giác \(MNC\) bằng \(\dfrac{1}{{12}}\) diện tích hình chữ nhật $ABCD$.
Diện tích tam giác \(MNC\)là:
\(96:12 = 8\;(c{m^2})\)
Diện tích tam giác \(AMN\)là:
\(96 - (24 + 32 + 8) = 32\;(c{m^2})\)
Đáp số: \(32c{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(32\).
Luyện tập và củng cố kiến thức Ôn tập về hình học: Tính diện tích, thể tích một số hình Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập các phép tính với số đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về phép chia Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về phép nhân Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về phép trừ Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về phép cộng Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về số đo thời gian Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về đo diện tích và đo thể tích Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về đo độ dài và đo khối lượng Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về số thập phân Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về phân số Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập về số tự nhiên Toán 5 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
