-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA ĐA THỨC
-
Chủ đề 1 : Phép nhân đa thức – Hằng đẳng thức đáng nhớ
-
Chủ đề 2 : Phân tích đa thức thành nhân tử
- 1. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- 2. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- 3. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- 4. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
- Luyện tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
-
Chủ đề 3: Phép chia đa thức
-
Ôn tập chương 1 - Phép nhân và phép chia đa thức
-
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
-
CHƯƠNG 1. TỨ GIÁC
-
Chủ đề 1 : Tứ giác – Hình thang
-
Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- 1. Đối xứng trục
- 2. Hình bình hành
- 3. Đối xứng tâm
- 4. Hình chữ nhật
- 5. Tập hợp các điểm cách đều một đường thẳng cho trước
- 6. Hình thoi
- 7. Hình vuông
- Bài tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- Luyện tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
-
Ôn tập chương 1 - Tứ giác
-
-
CHƯƠNG 2. ĐA GIÁC. DIỆN TÍCH ĐA GIÁC
-
CHƯƠNG 3 : PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN – GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH
-
CHƯƠNG 4. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
-
CHƯƠNG 3. TAM GIÁC ĐỒNG DẠNG
-
Chủ đề 1 : Định lí Thales
-
Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- 1. Khái niệm hai tam giác đồng dạng
- 2. Trường hợp đồng dạng thứ nhất (c.c.c)
- 3. Trường hợp đồng dạng thứ hai (c.g.c)
- 4. Trường hợp đồng dạng thứ ba (g.g)
- 5. Các trường hợp đồng dạng của tam giác vuông
- 6. Ứng dụng thực tế của tam giác đồng dạng
- Bài tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- Luyện tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
-
-
CHƯƠNG 4 : HÌNH LĂNG TRỤ ĐỨNG – HÌNH CHÓP ĐỀU
-
ÔN TẬP CUỐI NĂM - TÀI LIỆU DẠY-HỌC TOÁN 8
Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8
4. Trường hợp đồng dạng thứ ba (g.g)
Hoạt động 7 trang 79 Tài liệu dạy – học Toán 8 tập 2
Giải bài tập Cho hai tam giác ABC và A’B’C’ có
Đề bài
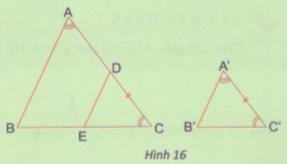
Cho hai tam giác ABC và A’B’C’ có \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\) (hình 16). Trên cạnh AC, lấy điểm D sao cho DC = A’C’. Qua D kẻ đường thẳng song song với AB cắt cạnh BC tại E.
- Tam giác DEF có đồng dạng với tam giác ABC không ?
- Nhận xét về mối quan hệ giữa tam giác A’B’C’ và tam giác DEC.
- Dự đoán về sự đồng dạng của hai tam giác A’B’C’ và tam giác ABC.
Lời giải chi tiết
\(\eqalign{ & a)DE//AB(gt) \Rightarrow \Delta DEC \sim \Delta ABC \cr & b)\widehat {EDC} = \widehat {BAC},\widehat {BAC} = \widehat {B'A'C'}\cr& \Rightarrow \widehat {B'A'C'} = \widehat {EDC} \cr} \)
Xét ∆A’B’C’ và ∆DEC có \(\widehat {B'A'C'} = \widehat {EDC},A'C' = DC(gt),\) \(\widehat {C'} = \widehat C(gt)\)
\( \Rightarrow \Delta A'B'C' = \Delta DEC(g.c.g)\)
c) \(\Delta A'B'C' \sim \Delta DEC\) \((\Delta A'B'C' = \Delta DEC)\) và \(\Delta DEC \sim \Delta ABC \) \(\Rightarrow \Delta A'B'C' \sim \Delta ABC\)
Loigiaihay.com
Bình luận
Chia sẻ
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3 bước: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
