Hoạt động 23 trang 125 Tài liệu dạy – học Toán 8 tập 1

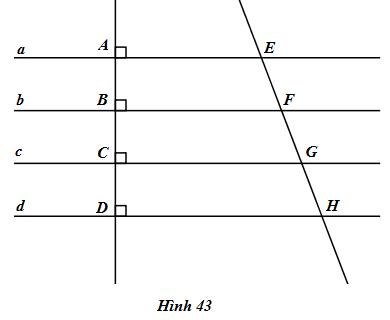
Giải bài tập Cho hình 43, trong đó các đường thẳng a, b, c, d song song với nhau.

Đề bài

Cho hình 43, trong đó các đường thẳng a, b, c, d song song với nhau.

Chứng minh rằng:

a) Nếu các đường thẳng a, b, c, d song song và cách đều thì EF = FG = GH.

b) Nếu EF = FG = GH thì các đường thẳng a, b, c, d song song và cách đều nhau.

Lời giải chi tiết

a) Hình thang AEGC (AE //GC) có:

\(\left. \matrix{ AB = BC \hfill \cr BF//AE//CG \hfill \cr} \right\} \Rightarrow EF = FG\)

Hình thang BFHD (BF // DH) có:

\(\left. \matrix{ BC = CD \hfill \cr CG//BF//DH \hfill \cr} \right\} \Rightarrow FG = GH\)

Vậy EF = FG = GH

b) Hình thang AEGC có:

\(\left. \matrix{ EF = FG \hfill \cr BF//AE//CG \hfill \cr} \right\} \Rightarrow AB = BC\)

Hình thang BFHD (BF // HD) có:

\(\left. \matrix{ FG = GH \hfill \cr CG//BF//DH \hfill \cr} \right\} \Rightarrow BC = CD\)

Ta có AB = BC = CD.

Do đó a, b, c, d là các đường thẳng song song và cách đều.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Thử tài bạn trang 125 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Ở hình 44, đường thẳng AD lần lượt vuông góc với AM, BN, CE, DF. Biết AB = BC = CD và MN = 35 cm. Tính MF.
Hoạt động 22 trang 124 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Ở hình 40, đường thẳng b (vạch đứt quãng) chia con đường thành 2 làn đường có chiều rộng bằng nhau.
Thử tài bạn trang 124 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cắt một tấm bìa cứng thành hình tam giác ABC. Cho đáy BC của tam giacschyeenr động trên đường thẳng a (h.41). Hỏi đỉnh A của tam giác chuyển dộng trên đường nào ?
Hoạt động 21 trang 123 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Một vận động viên xe đạp chạy xe trên một quảng đường phẳng (h.39). Hỏi trục A của bánh xe trước di động trên đường nào ?
Hoạt động 20 trang 123 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho hai đường thẳng song song a và b (h.37). Gọi A và B là hai điểm bất kì thuộc đường thẳng a; AH và BK là các đường vuông góc kẻ từ A và B đến đường thẳng b. Gọi độ dài AH là h. Tính độ dài BK theo h.
Hoạt động 19 trang 122 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Hình 36 cho biết quy định về việc kẻ vạch sơn đường dành cho người đi bộ. Em có nhận xét gì về khoảng cách các vạch sơn đó.