Giải bài tập Tài liệu Dạy - học Toán lớp 9, Phát triển tư duy đột phá trong dạy học Toán 9

1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trê..

Hoạt động 1 trang 68 Tài liệu dạy – học Toán 9 tập 1

Giải bài tập Xét tam giác vuông ABC vuông tại A, cạnh huyền BC = a, các cạnh góc vuông AC = b và

Đề bài

Xét tam giác vuông ABC vuông tại A, cạnh huyền BC = a, các cạnh góc vuông AC = b và \(AB = c\). Gọi AH = h là đường cao ứng với cạnh huyền và \(HC = b',HB = c'\) lần lượt là hình chiếu của AC, AB trên cạnh huyền BC.

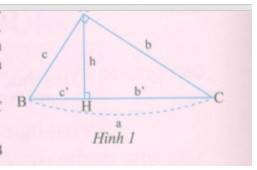
a) Chứng minh các tam giác HBA và ABC đồng dạng, từ đó so sánh \({c^2}\) và \(c'.a\).

b) Chứng minh các tam giác HCA và ACB đồng dạng, từ đó so sánh \({b^2}\) và \({b'}.a\).

Lời giải chi tiết

a) Chứng minh các tam giác HBA và ABC đồng dạng, từ đó so sánh \({c^2}\) và \(c'.a\).

Xét tam giác HBA và tam giác ABC có:

+) \(\widehat B\) chung;

+) \(\widehat {AHB} = \widehat {CAB} = {90^o}\)

\( \Rightarrow \) Tam giác HBA và ABC đồng dạng (g.g)

\( \Rightarrow \dfrac{{HB}}{{AB}} = \dfrac{{AB}}{{CB}}\)

hay \(\dfrac{{c'}}{c} = \dfrac{c}{a} \Leftrightarrow {c^2} = c'.a\)

b) Chứng minh các tam giác HCA và ACB đồng dạng, từ đó so sánh \({b^2}\) và \({b'}.a\).

Xét tam giác HCA và tam giác ACB có:

+) \(\widehat C\) chung;

+) \(\widehat {AHC} = \widehat {BAC} = {90^o}\)

\( \Rightarrow \) Tam giác HCA và ACB đồng dạng (g.g)

\( \Rightarrow \dfrac{{HC}}{{AC}} = \dfrac{{AC}}{{BC}}\)

hay \(\dfrac{{b'}}{b} = \dfrac{b}{a} \Leftrightarrow {b^2} = b'.a\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 5 phiếu

Bài tiếp theo

Thử tài bạn 1 trang 68 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Tìm x, y trong hình 2.
Bạn nào đúng 1 trang 68 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Theo em, bạn nào đúng ?

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục

TẢI APP ĐỂ XEM OFFLINE

Bài giải mới nhất