Bài tập trắc nghiệm trang 209, 210, 211 SBT đại số và giải tích 11
Giải bài tập trắc nghiệm trang 209, 210, 211 sách bài tập đại số và giải tích 11
Chọn đáp án đúng:
5.70
Tìm đạo hàm của hàm số \(y = \dfrac{{\sin {x^2}}}{x}\)
Lời giải chi tiết:
\(\begin{array}{l}y' = \dfrac{{\left( {\sin {x^2}} \right)'.x - \sin {x^2}.\left( x \right)'}}{{{x^2}}}\\ = \dfrac{{\left( {{x^2}} \right)'\cos {x^2}.x - \sin {x^2}}}{{{x^2}}}\\ = \dfrac{{2x\cos {x^2}.x - \sin {x^2}}}{{{x^2}}}\\ = \dfrac{{2{x^2}\cos {x^2} - \sin {x^2}}}{{{x^2}}}\end{array}\)
Chọn đáp án: A
5.71
Cho hàm số \(y = \cos \dfrac{x}{{x + 1}}\). Tìm y'
Lời giải chi tiết:
\(\begin{array}{l}y' = \left( {\dfrac{x}{{x + 1}}} \right)'\left( { - \sin \dfrac{x}{{x + 1}}} \right)\\ = \dfrac{{\left( x \right)'\left( {x + 1} \right) - x\left( {x + 1} \right)'}}{{{{\left( {x + 1} \right)}^2}}}\left( { - \sin \dfrac{x}{{x + 1}}} \right)\\ = \dfrac{{x + 1 - x}}{{{{\left( {x + 1} \right)}^2}}}\left( { - \sin \dfrac{x}{{x + 1}}} \right)\\ = \dfrac{{ - \sin \dfrac{x}{{x + 1}}}}{{{{\left( {x + 1} \right)}^2}}}\end{array}\)
Chọn đáp án: C
5.72
Tìm đạo hàm của hàm số y = tan2 x – cot x2
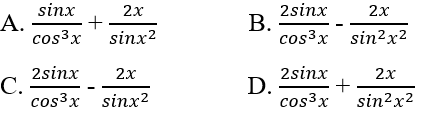
Lời giải chi tiết:
\(\begin{array}{l}y' = 2\tan x\left( {\tan x} \right)' - \left( {{x^2}} \right)'.\left( { - \dfrac{1}{{{{\sin }^2}{x^2}}}} \right)\\ = 2\tan x.\dfrac{1}{{{{\cos }^2}x}} + \dfrac{{2x}}{{{{\sin }^2}{x^2}}}\\ = 2.\dfrac{{\sin x}}{{\cos x}}.\dfrac{1}{{{{\cos }^2}x}} + \dfrac{{2x}}{{{{\sin }^2}{x^2}}}\\ = \dfrac{{2\sin x}}{{{{\cos }^3}x}} + \dfrac{{2x}}{{{{\sin }^2}{x^2}}}\end{array}\)
Chọn đáp án: D
5.73
Cho \(f\left( t \right) = \dfrac{{\cos t}}{{1 - \sin t}}\). Tính f'(π/6)
A. -2 B. -3 C. 2 D. 5
Lời giải chi tiết:
\(\begin{array}{l}f'\left( t \right)\\ = \dfrac{{\left( {\cos t} \right)'\left( {1 - \sin t} \right) - \cos t.\left( {1 - \sin t} \right)'}}{{{{\left( {1 - \sin t} \right)}^2}}}\\ = \dfrac{{ - \sin t\left( {1 - \sin t} \right) - \cos t\left( { - \cos t} \right)}}{{{{\left( {1 - \sin t} \right)}^2}}}\\ = \dfrac{{ - \sin t + {{\sin }^2}t + {{\cos }^2}t}}{{{{\left( {1 - \sin t} \right)}^2}}}\\ = \dfrac{{ - \sin t + 1}}{{{{\left( {1 - \sin t} \right)}^2}}}\\ = \dfrac{1}{{1 - \sin t}}\\ \Rightarrow f'\left( {\dfrac{\pi }{6}} \right) = \dfrac{1}{{1 - \sin \dfrac{\pi }{6}}}\\ = \dfrac{1}{{1 - \dfrac{1}{2}}} = 2\end{array}\)
Chọn đáp án: C
5.74
Tìm đạo hàm của hàm số y = (3 - sinx)3
A. 3(3 - sinx)
B. -3(3 - sinx)2cosx
C. -3(3 - sinx).cosx
D. -3(3 - sinx).cos2x
Lời giải chi tiết:
\(\begin{array}{l}y' = 3{\left( {3 - \sin x} \right)^2}\left( {3 - \sin x} \right)'\\ = 3{\left( {3 - \sin x} \right)^2}\left( {0 - \cos x} \right)\\ = - 3{\left( {3 - \sin x} \right)^2}\cos x\end{array}\)
Chọn đáp án: B
5.75
Cho \(f\left( x \right) = \sqrt {1 + 2\tan x} \). Tính f'(π/4)

Lời giải chi tiết:
\(\begin{array}{l}f'\left( x \right) = \dfrac{{\left( {1 + 2\tan x} \right)'}}{{2\sqrt {1 + 2\tan x} }}\\ = \dfrac{{2.\left( {\tan x} \right)'}}{{2\sqrt {1 + 2\tan x} }}\\ = \dfrac{{\dfrac{1}{{{{\cos }^2}x}}}}{{\sqrt {1 + 2\tan x} }}\\ = \dfrac{1}{{{{\cos }^2}x\sqrt {1 + 2\tan x} }}\\ \Rightarrow f'\left( {\dfrac{\pi }{4}} \right) = \dfrac{1}{{{{\cos }^2}\dfrac{\pi }{4}\sqrt {1 + 2\tan \dfrac{\pi }{4}} }}\\ = \dfrac{1}{{{{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}.\sqrt {1 + 2.1} }} = \dfrac{2}{{\sqrt 3 }} = \dfrac{{2\sqrt 3 }}{3}\end{array}\)
Chọn đáp án: D
5.76
Tìm đạo hàm của \(g\left( \varphi \right) = \dfrac{{\cos \varphi + \sin \varphi }}{{1 - \cos \varphi }}\)
Lời giải chi tiết:
\(\begin{array}{l}g'\left( \varphi \right)\\ = \dfrac{{\left( {\cos \varphi + \sin \varphi } \right)'\left( {1 - \cos \varphi } \right) - \left( {\cos \varphi + \sin \varphi } \right)\left( {1 - \cos \varphi } \right)'}}{{{{\left( {1 - \cos \varphi } \right)}^2}}}\\ = \dfrac{{\left( { - \sin \varphi + \cos \varphi } \right)\left( {1 - \cos \varphi } \right) - \left( {\cos \varphi + \sin \varphi } \right)\left( { - \left( { - \sin \varphi } \right)} \right)}}{{{{\left( {1 - \cos \varphi } \right)}^2}}}\\ = \dfrac{{ - \sin \varphi + \cos \varphi + \sin \varphi \cos \varphi - {{\cos }^2}\varphi - \cos \varphi \sin \varphi - {{\sin }^2}\varphi }}{{{{\left( {1 - \cos \varphi } \right)}^2}}}\\ = \dfrac{{ - \sin \varphi + \cos \varphi - \left( {{{\cos }^2}\varphi + {{\sin }^2}\varphi } \right)}}{{{{\left( {1 - \cos \varphi } \right)}^2}}}\\ = \dfrac{{\cos \varphi - \sin \varphi - 1}}{{{{\left( {1 - \cos \varphi } \right)}^2}}}\end{array}\)
Chọn đáp án: A
5.77
Cho \(y = \cot \sqrt {1 + {x^2}} \). Tính y'(1)
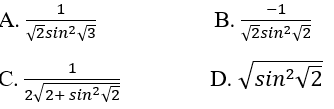
Lời giải chi tiết:
\(\begin{array}{l}y' = \left( {\sqrt {1 + {x^2}} } \right)'.\left( { - \dfrac{1}{{{{\sin }^2}\sqrt {1 + {x^2}} }}} \right)\\ = \dfrac{{\left( {1 + {x^2}} \right)'}}{{2\sqrt {1 + {x^2}} }}.\left( { - \dfrac{1}{{{{\sin }^2}\sqrt {1 + {x^2}} }}} \right)\\ = \dfrac{{2x}}{{2\sqrt {1 + {x^2}} }}.\left( { - \dfrac{1}{{{{\sin }^2}\sqrt {1 + {x^2}} }}} \right)\\ = - \dfrac{x}{{\sqrt {1 + {x^2}} .{{\sin }^2}\sqrt {1 + {x^2}} }}\\ \Rightarrow y'\left( 1 \right) = - \dfrac{1}{{\sqrt 2 {{\sin }^2}\sqrt 2 }}\end{array}\)
Chọn đáp án: B
5.78
Cho f(x) = 5x2 - 16√x + 7. Tính f'(4); f'(1/4)
A. 36; -27/2
B. -36; 27/2
C. 1; 35
D. 36; -2
Lời giải chi tiết:
\(\begin{array}{l}f'\left( x \right) = 5.2x - 16.\dfrac{1}{{2\sqrt x }}\\ = 10x - \dfrac{8}{{\sqrt x }}\\ \Rightarrow f'\left( 4 \right) = 10.4 - \dfrac{8}{{\sqrt 4 }} = 36\\f'\left( {\dfrac{1}{4}} \right) = 10.\dfrac{1}{4} - \dfrac{8}{{\sqrt {\dfrac{1}{4}} }} = - \dfrac{{27}}{2}\end{array}\)
Chọn đáp án: A
5.79
Cho g(x) = x2sin(x - 2). Tính g'(2).
A. -2 B. 4 C. 2 D. 1
Lời giải chi tiết:
\(\begin{array}{l}
g'\left( x \right) = \left( {{x^2}} \right)'\sin \left( {x - 2} \right)\\
+ {x^2}\left[ {\sin \left( {x - 2} \right)} \right]'\\
= 2x\sin \left( {x - 2} \right) + {x^2}.\cos \left( {x - 2} \right)\\
\Rightarrow g'\left( 2 \right) = 2.2\sin 0 + {2^2}\cos 0\\
= 0 + 4.1 = 4
\end{array}\)
Chọn đáp án: B
5.80
Tìm đạo hàm của hàm số \(y = \tan \dfrac{x}{2} - \cot \dfrac{x}{2}\)
Lời giải chi tiết:
\(\begin{array}{l}y' = \left( {\dfrac{x}{2}} \right)'.\dfrac{1}{{{{\cos }^2}\dfrac{x}{2}}} - \left( {\dfrac{x}{2}} \right)'.\left( { - \dfrac{1}{{{{\sin }^2}\dfrac{x}{2}}}} \right)\\ = \dfrac{1}{2}.\dfrac{1}{{{{\cos }^2}\dfrac{x}{2}}} + \dfrac{1}{2}.\dfrac{1}{{{{\sin }^2}\dfrac{x}{2}}}\\ = \dfrac{1}{2}\left( {\dfrac{1}{{{{\cos }^2}\dfrac{x}{2}}} + \dfrac{1}{{{{\sin }^2}\dfrac{x}{2}}}} \right)\\ = \dfrac{1}{2}.\dfrac{{{{\sin }^2}\dfrac{x}{2} + {{\cos }^2}\dfrac{x}{2}}}{{{{\cos }^2}\dfrac{x}{2}.{{\sin }^2}\dfrac{x}{2}}}\\ = \dfrac{2}{{4{{\cos }^2}\dfrac{x}{2}.{{\sin }^2}\dfrac{x}{2}}}\\ = \dfrac{2}{{{{\left( {2\cos \dfrac{x}{2}\sin \dfrac{x}{2}} \right)}^2}}}\\ = \dfrac{2}{{{{\sin }^2}x}}\end{array}\)
Chọn đáp án: D
5.81
Giải phương trình f'(x) = g(x), biết
g(x) = sinx và f(x) = (2 - x2)cosx + 2x.sinx.
Lời giải chi tiết:
\(\begin{array}{l}f'\left( x \right)\\ = \left( {2 - {x^2}} \right)'\cos x + \left( {2 - {x^2}} \right)\left( {\cos x} \right)'\\ + 2\left( {\left( x \right)'\sin x + x\left( {\sin x} \right)'} \right)\\ = - 2x\cos x + \left( {2 - {x^2}} \right)\left( { - \sin x} \right)\\ + 2\left( {\sin x + x\cos x} \right)\\ = - 2x\cos x - 2\sin x + {x^2}\sin x\\ + 2\sin x + 2x\cos x\\ = {x^2}\sin x\\ \Rightarrow f'\left( x \right) = {x^2}\sin x\\f'\left( x \right) = g\left( x \right)\\ \Leftrightarrow {x^2}\sin x = \sin x\\ \Leftrightarrow {x^2}\sin x - \sin x = 0\\ \Leftrightarrow \left( {{x^2} - 1} \right)\sin x = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} - 1 = 0\\\sin x = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \pm 1\\x = k\pi ,k \in \mathbb{Z}\end{array} \right.\end{array}\)
Chọn đáp án: C
Loigiaihay.com







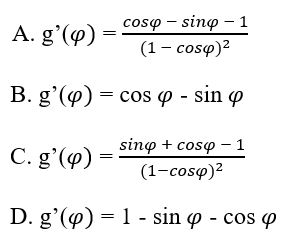
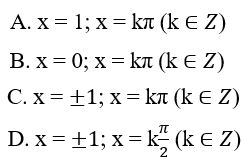








Danh sách bình luận