Giải bài tập, Sách bài tập (SBT) Toán 7 Bài 7. Đồ thị của hàm số y = ax (a khác 0)

Bài 57 trang 79 SBT toán 7 tập 1


Giải bài 57 trang 79 sách bài tập toán 7 tập 1. Một cạnh của hình chữ nhật là 5m, cạnh kia là x(m)....

Đề bài

Một cạnh của hình chữ nhật là \(5\,m\), cạnh kia là \(x\,(m)\). Hãy biểu diễn diện tích \(y\left( {{m^2}} \right)\) theo \(x\). Vẽ đồ thị của hàm số đó.

Từ đồ thị, hãy cho biết:

a) Diện tích của hình chữ nhật bằng bao nhiêu khi \(x = 2\,(m)? x = 3\,(m)?\)

b) Cạnh \(x\) bằng bao nhiêu khi diện tích \(y\) của hình chữ nhật bằng \(2,5\,({m^2})?\,5\,({m^2})?\)

Phương pháp giải - Xem chi tiết

- Công thức tính diện tích hình chữ nhật có chiều dài \(a\), chiều rộng \(b\) là: \(S=a.b\).

a) Từ các điểm \(x=2;3\) dựng các đường vuông góc với \(Ox\), từ giao điểm của đường này với đồ thị ta dựng đường vuông góc với \(Oy\) khi đó giao của đường vuông góc với \(Oy\) cho ta diên tích của hình chữ nhật.

b) Từ các điểm \(y=2,5;\,5\) dựng các đường vuông góc với \(Oy\), từ giao điểm của đường này với đồ thị ta dựng đường vuông góc với \(Ox\) khi đó giao của đường vuông góc với \(Ox\) cho ta độ dài cạnh \(x\) của hình chữ nhật.

Lời giải chi tiết

Diện tích của hình chữ nhật có cạnh là \(5\) m và cạnh kia \(x\) m là: \(y=5x\)

Vẽ đồ thị của hàm số \(y=5x\):

- Đồ thị đi qua \(O(0; 0)\)

- Cho \(x = 1 \Rightarrow  y = 5\), \( B(1; 5)\) thuộc đồ thị hàm số \(y=5x\).

- Vẽ đường thẳng \(OB\) ta có đồ thị của hàm số \(y=5x\).

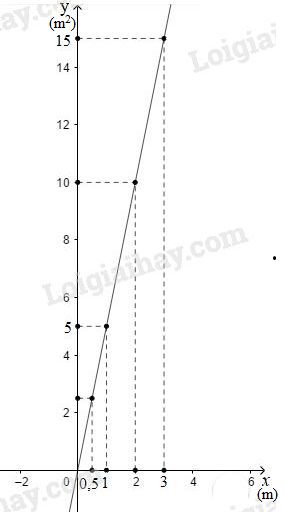
Bằng đồ thị ta xác định được:

\(\begin{array}{l}
a)\,f\left( 2 \right) = 10;f\left( 3 \right) = 5\\
b)\,y = 2,5 \Rightarrow x = \dfrac{1}{2}\\
y = 5 \Rightarrow x = 1
\end{array}\)

Kiểm tra bằng tính toán: 

a) Đặt \(y = f(x) = 5x\)

 Tại \(x = 2 \,(m);  x = 3\, (m)\) 

\(\eqalign{
& f\left( 2 \right) = 5.2 = 10({m^2}) \cr 
& f(3) = 5.3 = 15({m^2}) \cr} \)

b) Khi \(y = 2,5\,({m^2})\) \( \displaystyle \Rightarrow x = {y \over 5} = {{2,5} \over 5} = 0,5(m)\)

Khi \(y = 5({m^2})\) \(\displaystyle \Rightarrow x = {y \over 5} = {5 \over 5} = 1\left( m \right)\)

Loigiaihay.com


Bình chọn:
4.3 trên 10 phiếu
Bài tiếp theo

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store