-
ĐẠI SỐ SBT - TOÁN 10
-
HÌNH HỌC SBT - TOÁN 10
-
Chương 1: Véc tơ
-
Chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Bài 1: Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ
- Bài 2: Tích vô hướng của hai vec tơ
- Bài 3: Các hệ thức lượng trong tam giác và giải tam giác
- Ôn tập chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Ôn tập chương 2: Đề toán tổng hợp
- Câu hỏi trắc nghiệm chương 2: Tích vô hướng của hai véc tơ và ứng dụng
-
Chương 3: Phương pháp tọa độ trong mặt phẳng
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 2.33 trang 102 SBT hình học 10
Giải bài 2.33 trang 102 sách bài tập hình học 10. Chứng minh rằng...
Gọi \({m_a},{m_b},{m_c}\) là các trung tuyến lần lượt ứng với các cạnh a, b, c của tam giác ABC.
LG a
Tính \({m_a}\), biết rằng a = 26, b = 18, c = 16
Phương pháp giải:
Sử dụng công thức trung tuyến. Xem chi tiết tại đây.
Giải chi tiết:
\(m_a^2 = \dfrac{{{b^2} + {c^2}}}{2} - \dfrac{{{a^2}}}{4}\)\( = \dfrac{{{{18}^2} + {{16}^2}}}{2} - \dfrac{{{{26}^2}}}{4}\) \( = \dfrac{{324 + 256}}{2} - \dfrac{{676}}{4} = \dfrac{{484}}{4}\)\( \Rightarrow {m_a} = \dfrac{{22}}{2} = 11\)
LG b
Chứng minh rằng: \(4(m_a^2 + m_{_b}^2 + m_{_c}^2) = 3({a^2} + {b^2} + {c^2})\).
Phương pháp giải:
Sử dụng công thức trung tuyến. Xem chi tiết tại đây.
Giải chi tiết:
\(\left\{ \begin{array}{l}m_a^2 = \dfrac{{{b^2} + {c^2}}}{2} - \dfrac{{{a^2}}}{4}\\m_b^2 = \dfrac{{{a^2} + {c^2}}}{2} - \dfrac{{{b^2}}}{4}\\m_c^2 = \dfrac{{{a^2} + {b^2}}}{2} - \dfrac{{{c^2}}}{4}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}4m_a^2 = 2({b^2} + {c^2}) - {a^2}\\4m_b^2 = 2({a^2} + {c^2}) - {b^2}\\4m_c^2 = 2({a^2} + {b^2}) - {c^2}\end{array} \right.\)
Ta suy ra:
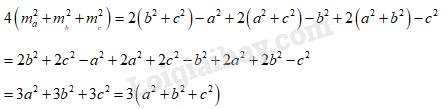
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 2.34 trang 102 SBT hình học 10
- Bài 2.35 trang 102 SBT hình học 10
- Bài 2.36 trang 102 SBT hình học 10
- Bài 2.37 trang 102 SBT hình học 10
- Bài 2.38 trang 102 SBT hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
